Capítulo 1 — Un jardín de enteros
Los enteros son la fuente de la que manan todas las matemáticas.
Hermann Minkowski, Diophantische Approximationen
Desde los albores de la civilización hemos utilizado los números enteros positivos para contar. Nadie sabe quién fue el primero en captar el concepto abstracto de, digamos, “siete”, como algo que se aplica tanto a un rebaño de siete cabras como a siete árboles, siete noches o a cualesquiera siete objetos. Los números de contar, junto con sus opuestos y el cero, forman el conjunto de los números enteros y ocupan un lugar central en las matemáticas. Es pues apropiado que comencemos con algunos teoremas y demostraciones sobre ellos.
En este capítulo presentamos varios resultados acerca de los enteros. Muchos se refieren a subconjuntos especiales de ellos, tales como los cuadrados perfectos, los números triangulares, los números de Fibonacci, los primos y los números perfectos. Aunque es posible demostrar la mayoría de los enunciados más simples mediante procedimientos algebraicos o por inducción, en la medida de lo posible preferimos presentar pruebas basadas en argumentos visuales. Comenzaremos contando el número de objetos que dan lugar a conjuntos asociados con patrones geométricos y estableceremos algunas identidades para ellos.
1.1. Números figurados
La idea de representar un número mediante puntos del plano (o, más probablemente, con piedrecitas en el suelo) se remonta al menos a la antigua Grecia. Cuando la representación toma la forma de un polígono, como un triángulo o un cuadrado, los números reciben a menudo el apelativo de figurados. Comenzamos con teoremas y demostraciones sobre los números más sencillos de este tipo: los números triangulares y los números cuadrados.
Casi todas las biografías del gran matemático Carl Friedrich Gauss (1777–1855) relatan la siguiente anécdota. Cuando Gauss tenía unos 10 años de edad, su profesor de Aritmética propuso a los alumnos de su clase que hicieran la suma \( 1 + 2 + 3 + 4 + \dots + 100 \),
suponiendo que así estarían ocupados durante un buen rato. Apenas terminó de plantear el problema, el joven Carl se levantó y colocó su tablilla en la mesa del profesor, sin cálculo alguno, con la respuesta correcta: 5050. Cuando este le pidió una explicación, Gauss le dijo que había reconocido el siguiente patrón: \(1 + 100 = 101\), \(2 + 99 = 101\), \(3 + 98 = 101\), ..., y así hasta \(50 + 51 = 101\). Como había cincuenta emparejamientos, la suma debía ser \(50 \times 101 = 5050\). El patrón geométrico que nos permite encontrar rápidamente este resultado (sumar el número más grande al más pformulaueño, el segundo más grande al segundo más pformulaueño, y así sucesivamente) se ilustra en la Figura 1.1, en la que las filas de bolas representan números enteros positivos.
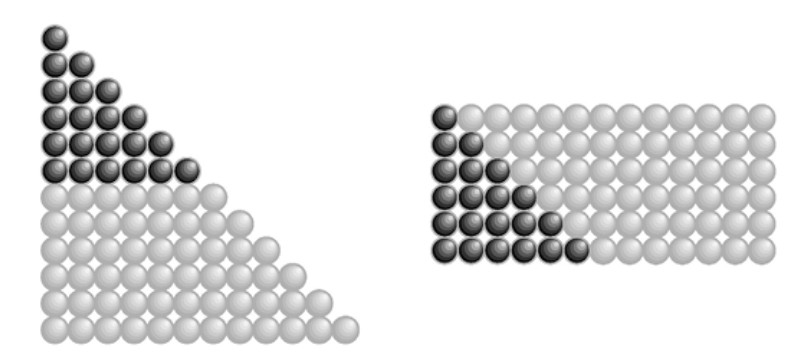
Llamaremos número triangular enésimo al número \(t_n = 1 + 2 + 3 + \cdots + n\), donde \(n\) es un entero positivo. Observando el patrón formado por los puntos de la imagen derecha de la Figura 1.1, el joven Carl obtuvo \(t_{100} = 5050\). Sin embargo, esta idea solo funciona si \(n\) es par, de forma que comenzaremos demostrando el siguiente resultado general:
Teorema 1.1. Para \(n \ge 1\), \(t_n = n \cdot (n + 1)/2\).
Demostración. Encontraremos un patrón que funcione para cualquier \(n\). Para ello encajamos dos copias de \(t_n\), como se muestra en la Figura 1.2, tras darle la vuelta a una de ellas. Así obtenemos un rectángulo formado por \(n\) filas de \(n + 1\) bolas cada una. Tenemos entonces que \(2 t_n = n \cdot (n + 1)\) y, por tanto, \(t_n = n \cdot (n + 1)/2\). ■

Como mencionamos en la introducción, el método de recuento utilizado en la demostración combinatoria anterior es conocido como recuento doble o de Fubini. Podemos usar el mismo procedimiento para probar que las sumas de números impares consecutivos, comenzando desde 1, son cuadrados perfectos.
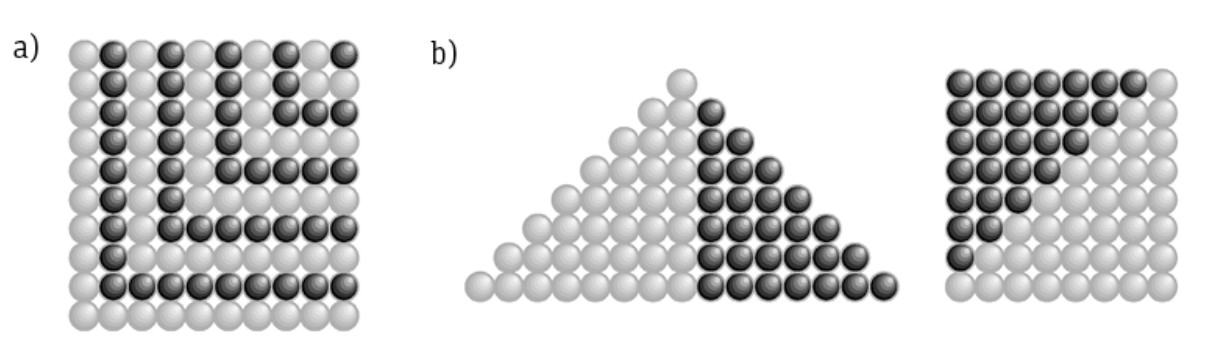
Teorema 1.2. Para \(n \ge 1\), \(1 + 3 + 5 + \cdots + (2n - 1) = n^2\).
Demostración. Damos dos pruebas combinatorias. La primera se muestra en la Figura 1.3a y consiste en contar las bolas de dos maneras; primero distribuyéndolas en forma de cuadrado y luego agrupándolas en filas. La Figura 1.3b muestra otra demostración, estableciendo una correspondencia uno a uno entre una distribución triangular formada por filas de 1, 3, 5, …, \(2n−1\) bolas y un cuadrado. ■
Podemos usar la misma idea en tres dimensiones para llegar a la siguiente secuencia de igualdades:
\(1 + 2 = 3\)
\(4 + 5 + 6 = 7 + 8\)
\(9 + 10 + 11 + 12 = 13 + 14 + 15\),
etc.
Como podemos ver, el número con el que empieza cada fila es un cuadrado perfecto. Es posible demostrar por inducción que, para cada entero positivo \(n\), se cumple siempre que
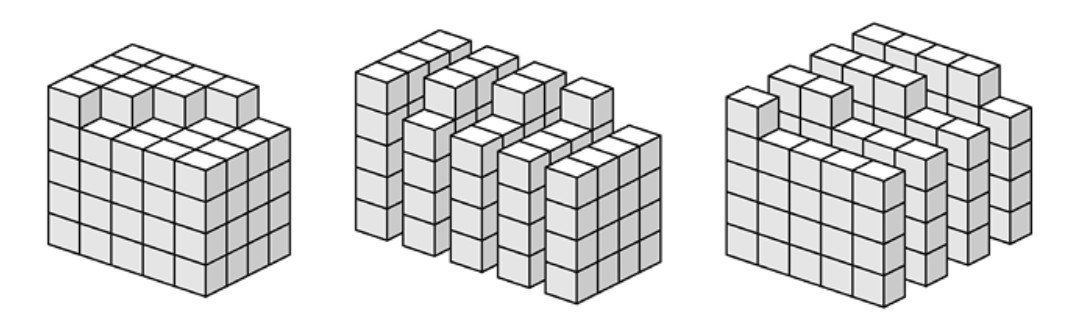
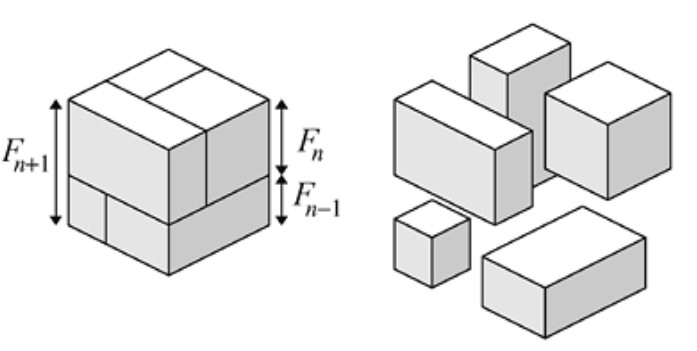
Pero la siguiente demostración visual tiene más encanto. En la Figura 1.4 vemos la versión para \(n = 4\) de esta igualdad. Contando el número de cubitos del volumen de la izquierda o de las figuras de la derecha, se obtiene que:
Hay muchas relaciones entre los números triangulares y los cuadrados. La más simple es, seguramente, la que se ilustra en la parte derecha de la Figura 1.3b: \( t_{n - 1} + t_n = n^2 \). Damos dos identidades más en el siguiente lema (tomando \( t_0 = 0 \) por conveniencia).
Lema 1.1. Para todo \( n \ge 0 \), (a) \( 8 t_n + 1 = (2n + 1)^2 \) y (b) \( 9 t_n + 1 = t_{3n+1} \).
Demostración. Véase la Figura 1.5 (donde hemos reemplazado bolas por cuadraditos). ■
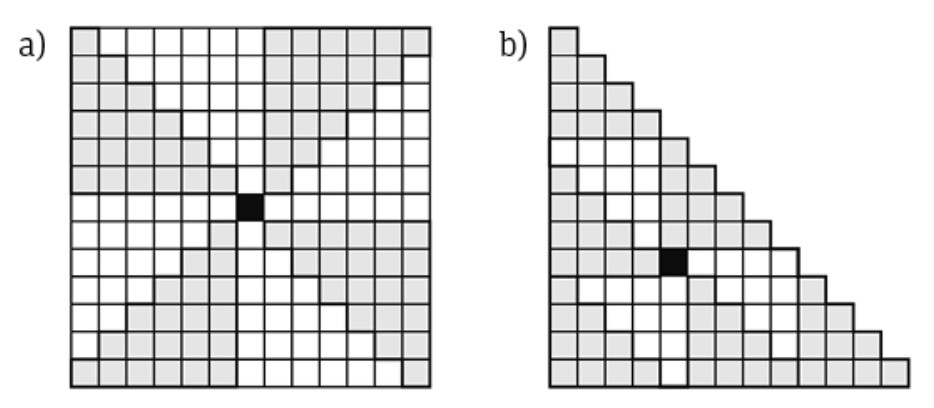
El Lema 1.1 nos permite demostrar los dos teoremas que enunciamos a continuación.
Teorema 1.3. Hay infinitos números que son a la vez triangulares y cuadrados.
Demostración. A partir de la identidad
\[ t_{8n} = \frac{8 t_n - (8t_n + 1)}{2} + 4 t_n = (2n + 1)^2, \]
podemos ver que, si \( t_n \) es un cuadrado, también lo es \( t_{8n} \). Como \( t_1 = 1 \) es un cuadrado perfecto, esta relación genera una sucesión infinita de números triangulares que son también cuadrados; por ejemplo: \( t_6 = 6^2 \), \( t_{288} = 204^2 \), etc. ■
Vemos, sin embargo, que hay números triangulares y cuadrados como, por ejemplo, \( t_{49} = 35^2 \) y \( t_{1188} = 1183^2 \) que no están en la lista anterior.
Teorema 1.4. Las sumas de las potencias de 9 son números triangulares, es decir, para todo \( n \ge 0 \), \( 1 + 9 + 9^2 + \cdots + 9^n = t_{1+3+3^2,\dots,3^n} \).
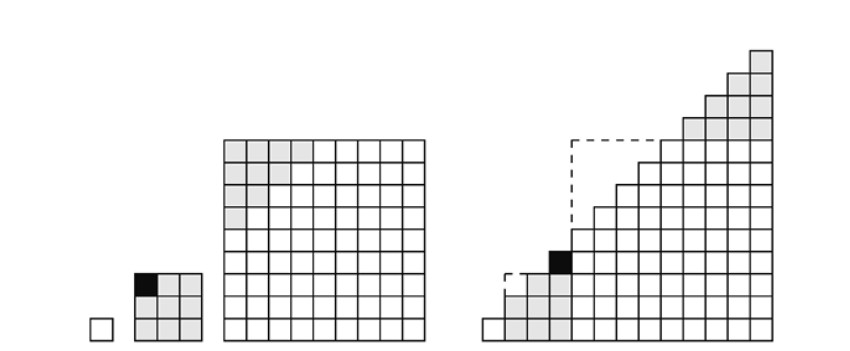
Demostración. Es fácil probar el teorema por inducción apoyándose en la identidad del Lema 1.1 (véase el Desafío 1.3), pero hay un argumento visual más elegante, que mostramos en la Figura 1.6. Una consecuencia interesante del resultado anterior es que, en base 9, los números 1, 11, 111, 1111, … son todos triangulares.
El teorema que viene a continuación hace buena pareja con la igualdad \( t_{n-1} + t_n = n^2 \).
Teorema 1.5. La suma de los cuadrados de dos números triangulares consecutivos es un número triangular, es decir, \( t_{n-1}^2 + t_n^2 = t_{n^2} \) para todo \( n \ge 1 \).
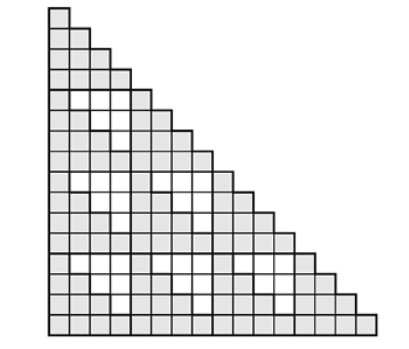
Demostración. Véase la Figura 1.7, donde se ilustra cómo representar y encajar los cuadrados de dos números triangulares para formar otro número triangular. ■
Quizá te hayas dado cuenta de que el enésimo número triangular es el número combinatorio \( t_n = \frac{n(n+1)}{2} \). Una forma de comprobarlo es ver que los dos miembros de la igualdad son \( n(n+1)/2 \), pero esta respuesta no aclara demasiado por qué es verdad. Una explicación mejor se obtiene recurriendo al principio de Cantor:
Teorema 1.6. Existe una correspondencia biunívoca entre un conjunto de \( t_n \) elementos y las formas de elegir dos objetos de un conjunto de \( n + 1 \) elementos.
Demostración. Véase la Figura 1.8 (Larson, 1985) y recuérdese que el coeficiente binomial \( \binom{n}{2} \) cuenta las formas de elegir dos elementos en un conjunto que tiene \( n \).
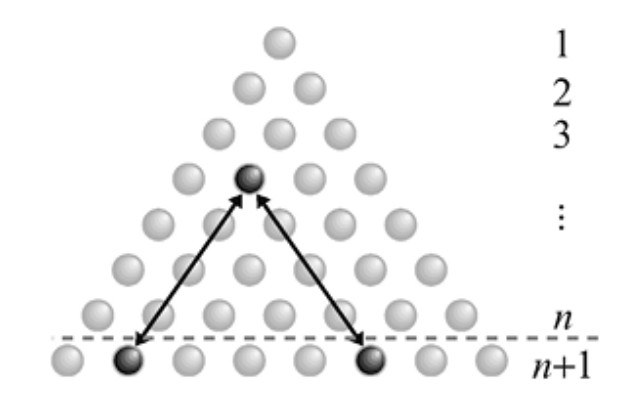
Las flechas marcan la correspondencia entre un elemento de un conjunto con \( t_n \) elementos y un par de elementos de un conjunto de \( n + 1 \) elementos (la última fila). ■
1.2. Sumas de cuadrados, cubos y números triangulares
Tras haber visto que podemos expresar los números triangulares y los cuadrados como sumas de enteros y sumas de enteros impares, ahora estudiaremos sumas de números triangulares y sumas de cuadrados.
Teorema 1.7. Para todo \( n \ge 1 \), \( 1^2 + 2^2 + 3^2 + \cdots + n^2 = n \cdot (n+1)\cdot (2n+1)/6. \)
Demostración. Damos dos; en la primera, mostramos una correspondencia biyectiva entre tres copias de \( 1^2 + 2^2 + 3^2 + \cdots + n^2 \) y el rectángulo de dimensiones \( 2n+1 \) por \( 1 + 2 + 3 + \cdots + n = n \cdot (n+1)/2 \) (Gardner, 1973). Véase la Figura 1.9.
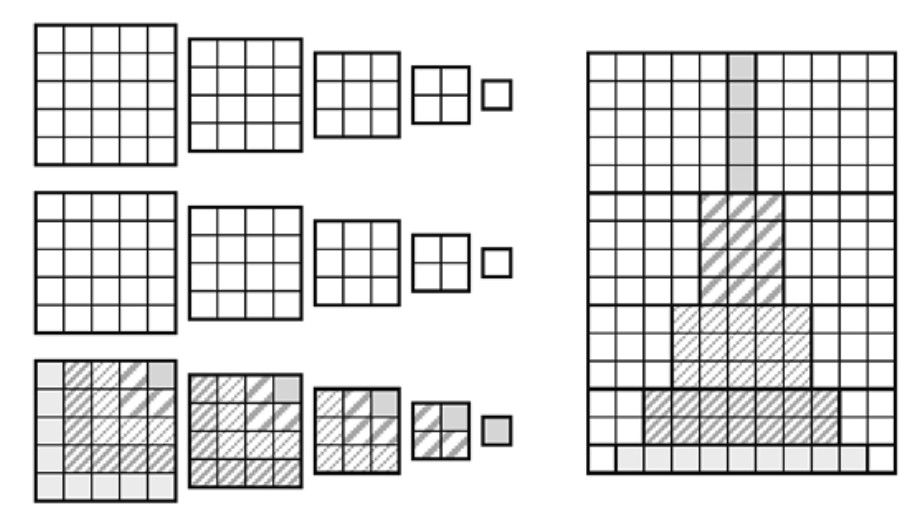
Así vemos inmediatamente que \( 3\cdot (1^2 + 2^2 + 3^2 + \cdots + n^2) = n(n+1)(2n+1)/2 \).
En la segunda demostración, escribimos cada número \( k^2 \) como suma de \( k \) veces \( k \), colocamos estos números formando un triángulo y construimos otros dos triángulos numéricos girando el primero 120° y 240°. Sumando término a término los números de esos tres triángulos, obtenemos otro en el que aparece el mismo número en todas las posiciones. Véase la Figura 1.10 (Kung, 1989). ■
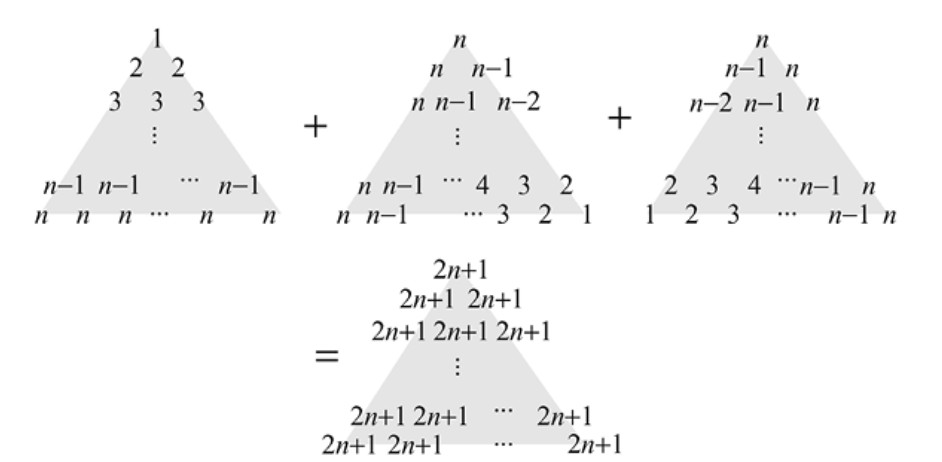
Teorema 1.8. Para todo \( n \ge 1 \), \[ t_1 + t_2 + t_3 + \cdots + t_n = n(n+1)(n+2)/6 \].
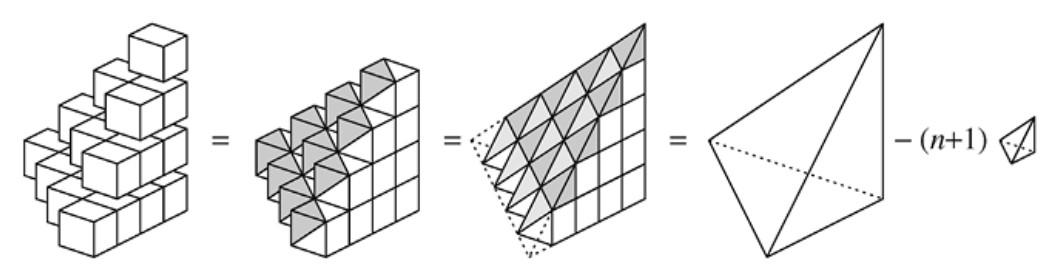
Demostración. Como se muestra en la Figura 1.11, apilamos capas de cubitos de volumen unidad, de forma que cada capa represente un número triangular. La suma de los números triangulares es igual al volumen de la pila de cubos.
Para calcular este volumen, rebanamos pformulaueñas pirámides (sombreadas en color gris) y las colocamos dándoles la vuelta encima del cubito del cual proceden (véase la Figura 1.11). El resultado es una pirámide recta triangular, de altura \( n \) en los dos lados de la base, cuyo volumen es igual al de la pirámide completa menos el volumen de \( n + 1 \) pirámides pformulaueñas (como las que faltan).
\[ t_1 + t_2 + t_3 + \cdots + t_n = \frac{1}{6}(n+1)^3 - \frac{1}{6}(n+1) = \frac{n(n+1)(n+2)}{6}. \]
En la demostración hemos obtenido la suma de los \( n \) primeros números triangulares calculando volúmenes de pirámides. Esta idea es una extensión del principio de Fubini en la que se usan longitudes, áreas y volúmenes como medidas naturales de objetos. El principio de Fubini para volúmenes establece que el volumen de un objeto formado por capas es igual a la integral del área de cada capa respecto a su altura. ■
Cantor a la suma de medidas porque es posible construir una correspondencia biyectiva entre los puntos de dos segmentos de distinta longitud.
Teorema 1.9. Para todo \( n \ge 1 \), \[ 1^2 + 2^2 + 3^2 + \cdots + n^2 - (1 + 2 + 3 + \cdots + n)^2 = t_n^2 . \]
Demostración. De nuevo damos dos pruebas. En la primera, representamos \[ k^2 \] como \( k \) copias de un cuadrado de área \[ k^2 \] para obtener la igualdad (Cupillari, 1989; Lushbaugh, 1965):
Fijándonos en la Figura 1.12, vemos que \[ 4(1^2 + 2^2 + 3^2 + \cdots + n^2) - [n(n+1)]^2. \]
Para la segunda demostración, usamos el hecho de que \[ 1 + 2 + 3 + \cdots + n + (n-1) + (n-2) + \cdots + 2 + 1 = n^2, \] (véase el Desafío 1.1a) y consideramos una distribución cuadrada de números donde el número que se encuentra en la fila \( i \) y la columna \( j \) es \[ ij. \] Sumamos ahora estos números de dos formas diferentes, como se muestra en la Figura 1.13 (Pourvousset, 1989).

Sumando por columnas, se obtiene: \[ \sum_{i=1}^{n} i + 2\sum_{i=1}^{n} i + \cdots + n\sum_{i=1}^{n} i = \left( \sum_{i=1}^{n} i \right)^2, \] mientras que sumando según las áreas sombreadas se llega a \[ 1\cdot1^2 + 2\cdot2^2 + 3\cdot3^2 + \cdots + n\cdot n^2 = \sum_{i=1}^{n} i^3. \]
Concluimos este apartado con un teorema que nos dice cómo representar un cubo como una suma doble de enteros.
Teorema 1.10. Para todo \( n \ge 1 \), \[ \sum_{i=1}^{n} \sum_{j=1}^{n} (i + j - 1) = n^3 . \]
Demostración. Representamos la suma doble como un conjunto de cubitos de volumen unidad y calculamos el volumen de una caja rectangular construida con dos copias de esta agrupación. Véase la Figura 1.14.
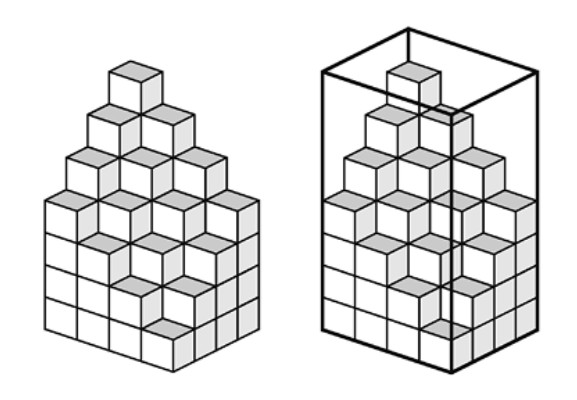
Dos copias de la suma \[ S = \sum_{i=1}^{n} \sum_{j=1}^{n} (i + j - 1) \] encajan formando una caja rectangular con base \( n^2 \) y altura \( 2n \), de aquí que dicha suma doble sea la mitad del volumen de la caja, es decir, \[ 2n \cdot n^2 / 2 = n^3. \] ■
1.3. Hay infinitos primos
La reducción al absurdo, que tanto gustaba a Euclides, es una de las armas más poderosas de las matemáticas. Va mucho más allá que el más audaz gambito de ajedrez: un jugador de ajedrez puede ofrecer el sacrificio de un peón, o incluso de una pieza menor, pero el matemático arriesga toda la partida.
G. H. Hardy, A Mathematician’s Apology
Seguramente la primera demostración de la existencia de infinitos primos es la que dio Euclides en los Elementos (libro IX, proposición 20). Aunque hayan transcurrido más de dos mil años, es difícil encontrar una mejor. Aquí presentamos tres pruebas diferentes. La primera, de 1873, es una demostración por reducción al absurdo. Se basa en un argumento debido a Ernst Eduard Kummer (1810–1893) y es muy elegante. La segunda es directa, e incluso más simple. Fue planteada por Henri Brocard (1845–1922) en 1915, aunque se le atribuyó a Charles Hermite (1822–1901) (Ribenboim, 2004). En la tercera demostración construimos números con un número arbitrario de factores primos distintos (Saidak, 2006).
La reducción al absurdo, que tanto gustaba a Euclides, es una de las armas más poderosas de las matemáticas.
Va mucho más allá que el más audaz gambito de ajedrez: un jugador de ajedrez puede ofrecer el sacrificio de un peón,
o incluso de una pieza mayor, pero el matemático arriesga toda la partida.
G. H. Hardy, A Mathematician’s Apology
Teorema de Euclides 1.11. Hay infinitos números primos.
Demostración 1: Supongamos que solo hay k números primos y que los ordenamos de menor a mayor, \(p_1, p_2, ..., p_k\). Sea \(N = p_1 p_2 \cdots p_k\). Como \(N + 1\) es más grande que todos esos primos, no es primo y entonces debe tener un factor primo q en común con N. Como q divide a N y a N + 1, debe dividir a su diferencia que es 1, lo que es absurdo. ■
Demostración 2: Basta con probar que para todo entero positivo n existe un primo p mayor que n. Esto lo cumple cualquier primo que divida a \(n! + 1\). ■
Demostración 3: Sea \(n > 1\) un número entero arbitrario. Dado que n y n+1 son consecutivos, han de ser primos entre sí, por tanto \(N_n = n(n+1)\) tiene al menos dos factores primos distintos. Del mismo modo, \(n(n+1)\) y \(n(n+1)+1\) son primos entre sí, luego \(N_{n+1} = n(n+1)[n(n+1)+1]\) debe tener, al menos, tres factores primos distintos. Continuando este proceso indefinidamente, se encuentran tantos números primos distintos como queramos. ■
Los primos de Euclides
Nos referimos al número \( N_p = p_1 p_2 \cdots p_n \) (el primorial de n). Los números \( E_n = N_n + 1 \) se llaman números de Euclides. Los cinco primeros son 3, 7, 31, 211 y 2311, y todos ellos son primos. Sin embargo, \(E_6 = 30\,031 = 59 \cdot 509\). No se sabe si hay infinitos números de Euclides.
En 1737, Leonhard Euler mostró que la suma de los inversos de los números primos diverge; por lo tanto, debe haber infinitos primos. Una prueba moderna aparece en F. Gillefeather y G. Meister (Leavitt, 1979), que resumimos a continuación.
Lema 1.2. La serie armónica \(1 + \frac12 + \frac13 + \cdots + \frac1n\) diverge.
Demostración: (Ward, 1970). Sea \( H_n = 1 + \frac12 + \frac13 + \cdots + \frac1n \) la enésima suma parcial de la serie armónica. Supongamos que la serie armónica converge a \(H\). En ese caso tendríamos \(\lim_{n\to\infty}(H_{2n}-H_n) - H - H = 0\). Pero se cumple la desigualdad:
de forma que \(\lim_{n\to\infty}(H_{2n}-H_n) \ne 0\), lo que conduce a una contradicción. ■
Teorema 1.12. \(\displaystyle \sum_{p\ \text{primo}} \frac{1}{p}\) diverge.
Demostración: Para un entero fijo \( n \ge 2 \), consideramos el conjunto de los primos \( p \le n \) y el producto
Como todo entero positivo \(k\) menor que \(n\) es un producto de potencias de primos menores que \(n\), para cada \(k\), su inverso \(1/k\) debe aparecer como sumando en el desarrollo del último producto. De aquí que
Dado que el logaritmo neperiano es una función creciente, al tomar logaritmos en la desigualdad anterior se mantiene:
Pero, por otro lado,
Combinando (1.1) y (1.2), obtenemos lo siguiente:
Como el lado de la derecha no está acotado cuando \( n \to \infty \), vemos que \(\displaystyle \sum_{p\ \text{primo}} \frac{1}{p}\) diverge. ■
Es posible encontrar más demostraciones en Vanden Eynden (1980).
Números primos y seguridad
Un aspecto gratificante de las matemáticas es la sorprendente aplicación de algunas de sus ramas. Durante siglos el estudio de los números primos estuvo motivado por cuestiones aritméticas de tipo fundamental. Pero ahora, en nuestra sociedad digital, donde toda la comunicación computacional está basada en el intercambio de números, los primos se han convertido en una herramienta básica para garantizar la seguridad y confidencialidad de los intercambios de información. Hoy día, muchos métodos usados en criptografía (el RSA de R. Rivest, A. Shamir y L. Adleman; el método de Elgamal o los de R. Merkle, W. Diffie y M. Hellman) se basan en propiedades de los números primos.
La idea clave en la que se fundamentan todos estos métodos es la enorme dificultad que conlleva factorizar el producto de dos números primos grandes.
1.4. Números de Fibonacci
Supongamos que tenemos una colección de cuadrados unitarios idénticos y de rectángulos de dimensiones \(1 \times 2\) que llamaremos dominós, y un \(n\)-marco (un rectángulo \(1 \times n\)). Denominamos \(f_n\) al número de formas distintas de recubrir un \(n\)-marco con cuadraditos y dominós sin que haya solapamientos. Por ejemplo, \(f_5 = 8\) (véase la Figura 1.15) porque podemos recubrir un \(5\)-marco de ocho formas distintas.
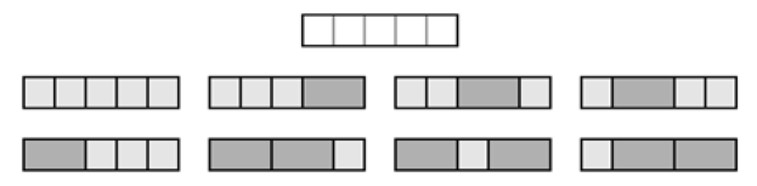
De forma similar, tenemos que \(f_1 = 1\), \(f_2 = 2\), \(f_3 = 3\), \(f_4 = 5\), \(f_5 = 8\), \(f_6 = 13\)... De hecho, es fácil ver que, para \(n \ge 3\), \(f_n = f_{n-1} + f_{n-2}\). En efecto, para recubrir un \(n\)-marco hemos de empezar, o bien con un cuadrado a la izquierda (y queda entonces por recubrir un \((n-1)\)-marco), o bien con un dominó, en cuyo caso falta por recubrir un \((n-2)\)-marco.
De esta observación se deduce que la regla de recurrencia que define la sucesión \(\{f_n\}\) es la misma que la de la sucesión de Fibonacci \(\{F_n\}\), \(F_n = F_{n-1} + F_{n-2}\) con \(F_1 = 1, F_2 = 1\). Si en nuestro problema hacemos \(f_0 = 0\) (para recubrir un 0-marco no hay que usar ni cuadrados ni dominós), tenemos que para \(n \ge 0\), \(f_n = F_{n+1}\).
Para probar resultados sobre los números de Fibonacci, basta con que lo hagamos para la sucesión \( \{ f_n \}_{n=1}^{\infty} \). Los dos teoremas siguientes y sus demostraciones están sacados de demostracions That Really Count (Benjamin y Quinn, 2003), una deliciosa colección de hermosas demostraciones sobre la sucesión de Fibonacci y otras relacionadas con ella. En todas se recurre al principio de Fubini, que consiste en contar los números de recubrimientos de \( n \)-marcos con cuadrados y dominós –sujetos a alguna condición particular– de dos maneras diferentes. Benjamin y Quinn llaman a este método condicionamiento.
Teorema 1.13.
Para n ≥ 0, \[ f_0 + f_1 + f_2 + \cdots + f_n = f_{n+2} - 1. \]
Demostración: ¿Cuántos recubrimientos de un \((n+2)\)-marco usan al menos un dominó? Evidentemente, una respuesta es \(f_{n+2} - 1\), ya que el único recubrimiento en el que no aparece ningún dominó es aquel en el que se usan exclusivamente cuadrados. Para la otra forma de contar, nos fijamos en la colocación del dominó que esté más a la izquierda (la condición en este ejemplo de condicionamiento). Si el recubrimiento de un \((n+2)\)-marco comienza a la izquierda con un dominó, el resto puede ser rellenado de \(f_n\) formas. Si el recubrimiento comienza a la izquierda por un cuadrado y luego viene un dominó, tenemos \(f_{n-1}\) formas de completarlo. Si el recubrimiento comienza con dos cuadrados, se puede completar de \(f_{n-2}\) formas, y así sucesivamente. Véase la Figura 1.16.
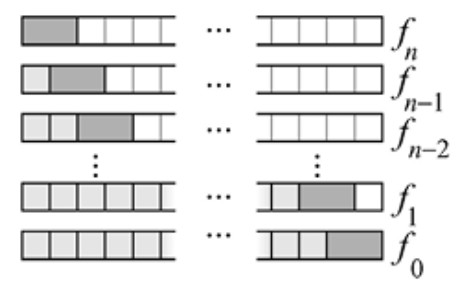
Continuamos hasta el caso final, en el que el recubrimiento consiste en \(n\) cuadrados y un dominó situado a su derecha, lo que solo se puede hacer de una forma \((f_0 = 1)\). ■
Teorema 1.14.
n ≥ 0, \[ f_0 + f_5 + f_{10} + \cdots + f_{2n} = f_{2n+1}. \]
Demostración: ¿Cuántos recubrimientos hay para un \((2n+1)\)-marco? La respuesta es \(f_{2n+1}\), por definición. Contemos de otra manera teniendo en cuenta ahora la colocación del cuadrado situado más a la izquierda. Si el recubrimiento de un \((2n+1)\)-marco comienza con un cuadrado, tenemos \(f_{2n}\) formas de completarlo. Si empieza a la izquierda con un dominó y luego viene un cuadrado, se debe completar de \(f_{2n-2}\) formas. Si el recubrimiento comienza a la izquierda con dos dominós, se podrá completar de \(f_{2n-4}\) formas. Véase la Figura 1.17.
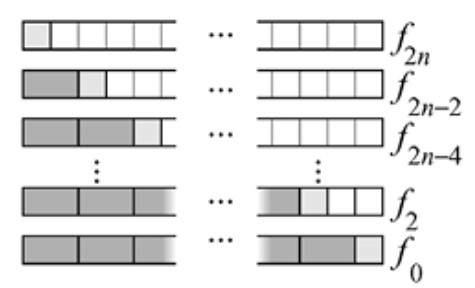
Continuamos así hasta el último paso, en el que el recubrimiento comienza con \(n\) dominós y acaba con un cuadrado, lo que solo se puede hacer de una forma \((f_0 = 1)\). ■
Véase demostracions That Really Count Benjamin y Quinn (2003) para aprender más sobre los números de Fibonacci y las demostraciones combinatorias.
Es posible ilustrar las demostraciones de algunas identidades en las que aparecen potencias de números de Fibonacci (como cuadrados y cubos) con diagramas en dos o tres dimensiones.
Teorema 1.15. Para n ≥ 1, \[ F_1^2 + F_2^2 + F_3^2 + \cdots + F_n^2 = F_n F_{n+1}. \]
Teorema 1.16. Para n ≥ 2, \[ F_{n+1}^3 = F_n^3 + F_{n-1}^3 + 3 F_{n-1} F_n F_{n+1}. \]
Parece sorprendente que no exista ninguna fórmula explícita para los números de Fibonacci que use solo números enteros, pero sí existe una en la que aparece el número de oro. Obtendremos la fórmula en el Apartado 2.3 del capítulo siguiente.
Números de Fibonacci por doquier
Leonardo de Pisa (ca. 1170–1240) quizá no supiera que sería conocido como Fibonacci (la contracción de filius Bonacci, “hijo de Bonaccio”), y seguro que nunca soñó que la sucesión 1, 1, 2, 3, 5, …, que él introdujo en un problema sobre contar conejos, llegaría a ser una sucesión tan célebre. La revista The Fibonacci Quarterly, aparecida en 1963, está dedicada al estudio de sus propiedades. Los números de Fibonacci aparecen con frecuencia en la naturaleza (filotaxis, girasoles, piñas de los pinos, piñas tropicales, alcachofas, árboles genealógicos de las abejas, etc.), al igual que en arquitectura y diseño.
1.5. El teorema de Fermat
Una de las herramientas más útiles en teoría de números es el resultado conocido como pformulaueño teorema de Fermat, denominado así para diferenciarlo del famoso gran o último teorema de Fermat. Pierre de Fermat (1601–1665) lo mencionó (sin demostración) en una carta de 1640; Leonhard Euler publicó la primera demostración en 1736. Hay muchas pruebas del teorema de Fermat. La que presentamos aquí es particularmente elegante. Se basa simplemente en contar cuerdas y un conjunto (Golomb, 1956).
Teorema de Fermat 1.17. Si n es entero y p primo, entonces p divide a \( n^p - n \). Además, si n no es múltiplo de p, entonces p divide a \( n^{p-1} - 1 \).
Demostración: Basta con probar el teorema para enteros positivos (véase el Desafío 1.7). Supongamos que tenemos un montón de cuentas de collar de n colores distintos y queremos fabricar collares multicolores con p cuentas. Enhebramos p cuentas en un cordel. Dado que cada cuenta puede escogerse de n colores, hay \( n^p \) posibles cuerdas de cuentas. Para cada una de los n colores hay un collar con todas las cuentas de ese color. Descartamos esos n collares monocromos, quedándonos con \( n^p - n \) collares. Unimos los extremos de los cordeles para obtener collares de forma que las cuentas puedan atravesar el punto inicial del cordel. Observemos, por ello, que dos collares son indistinguibles si se diferencian solo en el orden cíclico de sus cuentas. Agrupamos los cordeles no monocromos que caen dentro del mismo collar. Si p es primo, cada grupo se compone exactamente de p cordeles distintos (esto no sería cierto si p fuera compuesto, ¿por qué?), y por tanto, hay en total \( (n^p - n) / p \) collares distintos. En particular, \( (n^p - n)/p \) debe ser entero. Finalmente, como \( n^p - n = n(n^{p-1} - 1) \), si p no divide a n, entonces debe dividir a \( n^{p-1} - 1 \). ■
1.6. El teorema de Wilson
En el lenguaje de las congruencias, el teorema de Fermat se enuncia como sigue: si n es entero y p primo, entonces \( n^p \formulauiv n \pmod p \). Además, si n no es múltiplo de p, entonces \[ n^{p-1} \formulauiv 1 \pmod p. \]
Teorema de Wilson 1.18. Si p es primo, entonces \( (p-1)! \formulauiv -1 \pmod p \).
Demostración: El teorema es cierto para \( p = 2 \), de forma que en adelante supondremos que \( p \) es impar. Utilizaremos el teorema de Fermat, vemos que los enteros \( x = 1, 2, \ldots, p-1 \) son soluciones de la congruencia \( x^{p-1} \formulauiv 0 \pmod p \). Dado que una congruencia polinómica de grado \( p - 1 \) tiene exactamente \( p - 1 \) soluciones no congruentes entre sí módulo \( p \), tenemos que \[ x^{p-1} - 1 = (x - 1)(x - 2)\cdots(x - (p - 1)) \pmod p. \] Si comparamos los términos constantes en ambos lados de la expresión anterior, vemos que \[ -1 = (-1)(-2)\cdots(-(p-1)) = -(p-1)! \pmod p, \] lo que implica que \[ (p-1)! \formulauiv -1 \pmod p. \] ■
1.7. Números perfectos
Los números perfectos han atraído la atención de los matemáticos en cada siglo de la era cristiana.
L. E. Dickson, History of the Theory of Numbers
Los números perfectos, como los hombres perfectos, son muy escasos.
René Descartes
Un número perfecto es un entero positivo que es igual a la suma de sus divisores positivos estrictamente menores que él. Por ejemplo, 6 y 28 son perfectos, ya que \( 6 = 1 + 2 + 3 \) y \( 28 = 1 + 2 + 4 + 7 + 14 \). En la proposición 36 del libro IX de los Elementos, Euclides nos dice cómo construir números perfectos.
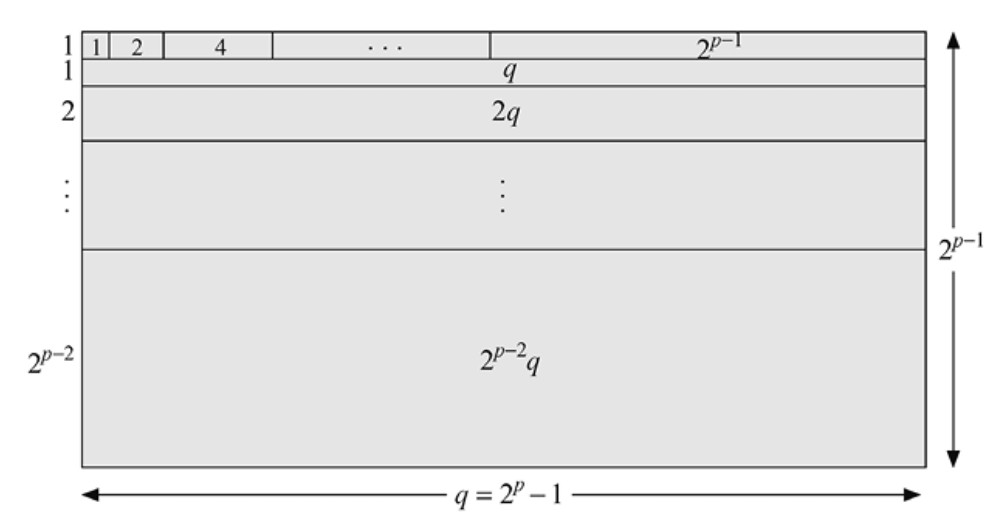
Teorema 1.19. (Euclides). Si \( p \) y \( q = 2^p - 1 \) son ambos primos, entonces \( 2^{p-1} q \) es perfecto.
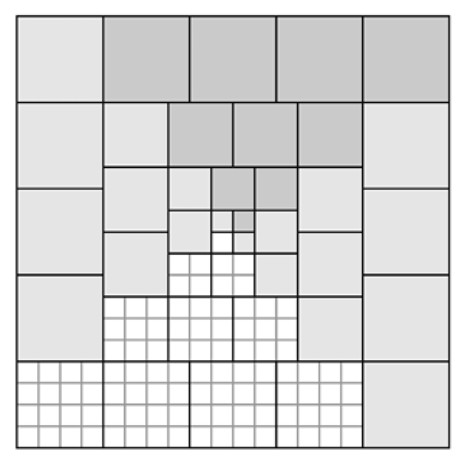
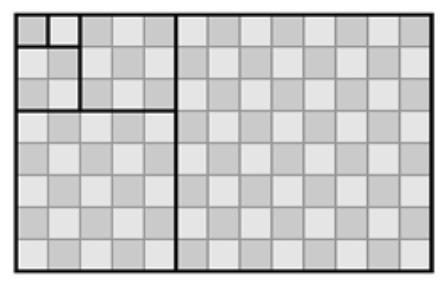
Demostración: Los divisores de \( 2^{p-1} q \) menores que él son \( \{1, 2, 2^2, \ldots, 2^{p-1};\; q, 2q, 2^2 q, \ldots, 2^{p-2}q\} \). En la Figura 1.20 podemos ver cómo disponer cuadrados y rectángulos cuyas áreas son esos divisores dentro de un rectángulo de área \( 2^{p-1} q \) (Goldberg). ■
Aproximadamente dos mil años después de Euclides, Leonard Euler (1707–1783) probó el recíproco del Teorema 1.19, es decir, que todo número par perfecto debe ser de la forma \( 2^{p-1} q \), con \( q = 2^p - 1 \) primo. Merece la pena subrayar que todo número perfecto par es un número triangular. No se sabe si existen números perfectos impares.
1.8. Desafíos
1.1. Usar un argumento combinatorio para probar que
a) \( 1 + 2 + 3 + \cdots + (n - 1) + n + (n - 1) + (n - 2) + \cdots + 2 + 1 = n^2 \).
b) \( 1 + 3 + 5 + \cdots + (2n - 1) + (2n + 1) + (2n - 1) + \cdots + 3 + 1 = n^2 + (n + 1)^2 \).
c) \[ \sum_{k=1}^{n} k^2 = \sum_{i=1}^{n} \sum_{j=1}^{n} \min(i,j). \]
1.2. Encontrar demostraciones visuales para a) \( 3 t_n + t_{n-1} = t_{2n} \), b) \( 3 t_n + t_{n+1} = t_{2n+1} \) y c) \( t_n + t_{n+1} + 6 t_n + t_{n+1} = (2n+1)^2 \).
1.3. Probar por inducción la identidad del Teorema 1.4.
1.4. Probar que hay infinitas parejas de números triangulares cuya suma es un número triangular.
1.5. ¿Puede un número de Euclides ser un cuadrado?
1.6. Sea \( F_n \) el enésimo número de Fibonacci. Probar que, para \( n \ge 2 \),
\[ F_{2n+1}^2 = 2 F_n \cdot F_{n-1} \cdot F_{2n} + F_{n-1}^2. \]
(Indicación: basta con una sola figura para este desafío).
1.7. Sea \( F_n \) el enésimo número de Fibonacci. Probar con una figura similar a la 1.18 que \( F_1 + F_3 + F_5 + \cdots + F_{2n} = F_2^2 + F_3^2 + \cdots + F_{2n-1}^2 = F_{2n} - F_{2n-1} \).
1.8. Sea \( F_n \) el enésimo número de Fibonacci. Probar la identidad de Cassini: para \( n \ge 2 \),
\[ F_{n+1} F_{n-1} - F_n^2 = (-1)^n. \]
(Indicación: demostrar primero que para \( n \ge 2 \), \( F_{n+1} = F_{n-1} F_{n-2} = F_{n-1} - F_n^2 \). Existe también un argumento visual.)
1.9. Se define la sucesión \( \{a_n\} \) de enteros positivos como sigue: \( a_1 = q,\; a_n = 2q,\; a_1 \ge 1 \) para \( n \ge 3 \). Encontrar una expresión explícita para \( a_n \). (Indicación: la base no es siempre la mejor).
1.10. Probar que el teorema de Fermat 1.17 se cumple para todos los enteros negativos \( n \).
1.11. Dado un entero positivo \( n \), \( \sigma(n) \) denota el número de divisores de \( n \). Por definición, \( n \) es primo si \( \sigma(n) = 2 \). Probar que \( n \) es un cuadrado si y solo si \( \sigma(n) \) es impar.
1.12. Sea \( n \) cualquier número perfecto mayor que 6. Probar que
a) \( n \) es de la forma \( 9a + 1 \);
b) Cuando \( n > 28 \), \( (n - 1)/9 \) no es primo.
Capítulo 2 — Números ilustres
El número, la invención por excelencia.
Esquilo, Prometeo encadenado
Los números son cosas terribles.
Eurípides, Hécuba
Dondformulauiera que haya un número, hay belleza.
Proclo
Los números no son solo bellos; son populares, tan populares que algunas de sus biografías han sido publicadas. He aquí una pformulaueña lista de ellas:
- e: The Story of a Number (Maor, 1994).
- The Joy of π (Blatner, 1997).
- The Golden Ratio and Fibonacci Numbers (Dunlap, 1997).
- The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number (Livio, 2002).
- An Imaginary Tale: The Story of i (Nahin, 1998).
- Gamma: Exploring Euler’s Constant (Havil, 2003).
- The Square Root of Two (Flannery, 2006).
En este capítulo probaremos varios resultados básicos sobre algunos números especiales como \(\sqrt{2}\), \(\pi\) y \(e\) . Las demostraciones elegidas, así como los propios números, son considerados bellos por muchos.
Nombres ilustres para números ilustres
Los números ilustres no son solo importantes, también tienen nombre. A \(\sqrt{2}\) se le llama, a veces, constante de Pitágoras por ser Pitágoras el primero que probó su irracionalidad. \(\pi\) recibe el nombre de constante de Arquímedes, debido a que Arquímedes estableció la desigualdad \( \tfrac{310}{71} < \pi < \tfrac{22}{7} \). También recibe el nombre de constante de Ludolph en honor a Ludolph van Ceulen (1540–1610), que dedicó muchos años a calcular los primeros treinta y cinco cifras decimales. A \(e\) se le conoce como constante de Euler, aunque a veces este nombre también se usa para \(\gamma\), la constante de Euler–Mascheroni. Dado que John Napier (1550–1617) casi descubrió el número \(e\), este también recibe el nombre de constante de Napier.
2.1. La irracionalidad de \( \sqrt{2} \)
Hay muchas demostraciones de que \( \sqrt{2} \) es irracional. Seguramente la más conocida es la demostración de Euclides, basada en el teorema de Pitágoras. Es también la más antigua, aunque hay otras que son más simples. Aquí presentamos una versión de otra vieja demostración de la irracionalidad de \( \sqrt{2} \) (Bloom, 1995):
Teorema 2.1. \( \sqrt{2} \) es irracional.
Demostración. Si \( \sqrt{2} \) fuera racional, es decir, si \( 1 < \sqrt{2} = \tfrac{m}{n} < 2 \), con \( m \) y \( n \) enteros positivos más pformulaueños posible, tendríamos entonces que \( \tfrac{1}{\sqrt{2}} = \tfrac{\sqrt{2}}{2} = \tfrac{m}{2n} \) y, por tanto, también \( \sqrt{2} = \tfrac{2n}{m} \).
Restando numeradores y denominadores, obtenemos que \( \sqrt{2} = \tfrac{2n-m}{m-n} \), que es una contradicción ya que \( 2n - m \) y \( m - n \) son positivos y estrictamente menores que \( m \) y \( n \). ■
Es seguramente más fácil entender la prueba si se ve de forma geométrica (Apostol, 2000). Si la fracción irreducible \( m/n \) es igual a \( \sqrt{2} \), entonces el triángulo rectángulo isósceles de lados \( n,n \) y \( m \) es el triángulo rectángulo isósceles más pformulaueño con esa propiedad. Sin embargo, si este es un triángulo rectángulo isósceles con lados enteros, entonces hay uno más pformulaueño con la misma propiedad.
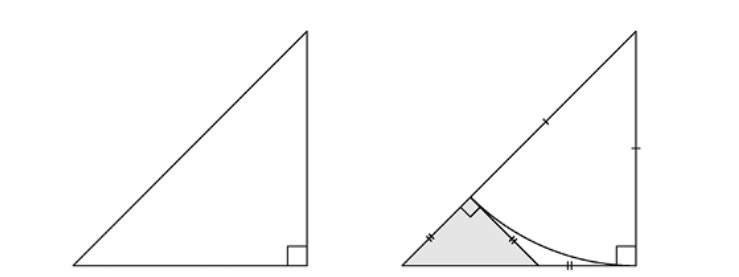
En efecto, si los lados del triángulo mayor son \( n, n \) y \( m \), entonces los lados del triángulo sombreado de la derecha son \( n - m, n - n \) y \( 2n - m \). Así, la suposición de que \( \sqrt{2} = m/n \) con \( m \) y \( n \) lo más pformulaueños posibles es falsa y llegamos a una contradicción, por lo que \( \sqrt{2} \) es irracional.
Hipaso y la irracionalidad de \( \sqrt{2} \)
Demostrar teoremas no suele ser peligroso. Al contrario, lo normal es que sea gratificante, pero en los días de Pitágoras la situación pudo haber sido diferente. Cuenta la leyenda que Hipaso de Metaponto (ca. 500 a. C.) descubrió la insospechada irracionalidad de \( \sqrt{2} \), explicó el resultado y por ello fue arrojado por la borda por sus hermanos pitagóricos. Este descubrimiento acabó con la idea de que en geometría todas las cantidades son conmensurables. Afortunadamente, la historia no ha registrado más muertes asociadas a la demostración de un teorema.
2.2. La irracionalidad de \( \sqrt{k} \) cuando \( k \) no es un cuadrado perfecto
Podemos modificar la demostración de la irracionalidad de \( \sqrt{2} \) para probar que también \( \sqrt{k} \) es irracional cuando \( k \) no es el cuadrado de un entero. En esta demostración, interpretamos \( \sqrt{k} \) como la pendiente de una recta que pasa por el origen, como se muestra en la Figura 2.2.
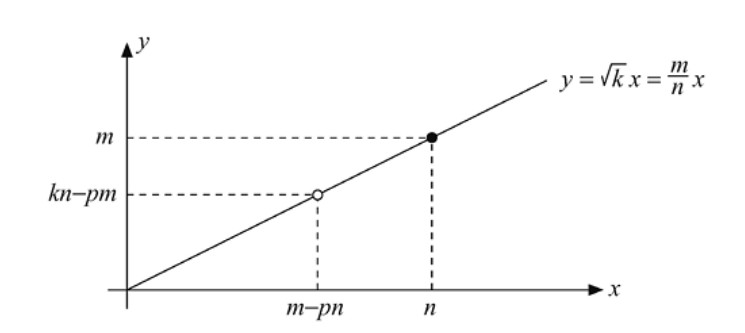
Teorema 2.2. Si \( k \) no es el cuadrado de un entero, entonces \( \sqrt{k} \) es irracional.
Demostración. Supongamos que en forma de fracción irreducible tenemos \( \sqrt{k} = m/n \). Entonces, el punto de la recta \( y = \sqrt{k}\, x \) con coordenadas enteras positivas más cercanas al origen es \( (n, m) \). Sea entonces \( p \) el mayor entero menor que \( \sqrt{k} \), es decir, \( p < \sqrt{k} < p + 1 \). Se tiene que el punto \( (m - pn, kn - pm) \) se encuentra también en la recta y está más cerca del origen, ya que \( (m/n) - (p/n) = (m - pn)/n \) pero \( kn - pm > 0 \) y \( p < m/n < p + 1 \) implica que \( 0 < kn - pm < n \) y \( 0 < m - pn < m \). Llegamos así a una contradicción y, por tanto, \( \sqrt{k} \) es irracional. ■
En base 10 es fácil probar que \( \sqrt{10} \) es irracional. Si \( \sqrt{10} = m/n \) en forma de fracción irreducible, tendríamos que \( m^2 = 10 n^2 \), pero el cuadrado de un número en base 10 acaba siempre en un número par de ceros, por lo que \( m^2 \) tendría que acabar a la vez en un número par y en un número impar de ceros, lo que es imposible.
2.3. La razón áurea
¿Cuál es la forma rectangular estéticamente más agradable? Algunas personas (aunque seguramente no todas) dirán que un rectángulo como el de la Figura 2.3a, donde el lado pformulaueño mide 1, y el grande mide \( \varphi \). Este rectángulo áureo tiene la propiedad de que, al quitarle un cuadrado (como se ve en la Figura 2.3b), el rectángulo resultante es semejante al de partida y se puede continuar indefinidamente este proceso (véase la Figura 2.3c).
Como deducimos a partir de la Figura 2.3b, se debe cumplir que \[ \frac{\varphi}{1} = \frac{1}{\varphi - 1}. \]
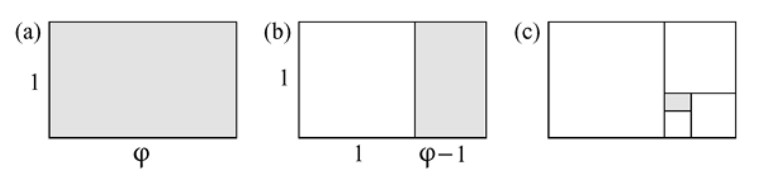
Así, vemos que se tiene que cumplir que \( \varphi^2 = \varphi + 1 \). Esta ecuación de segundo grado tiene dos soluciones, pero solo una es positiva, de forma que \[ \varphi = \frac{1 + \sqrt{5}}{2} \approx 1{,}618. \] Este número es conocido como razón áurea o proporción áurea. En la definición 3 y en la proposición 30 del libro VI de los Elementos, Euclides se refirió a la división de un segmento en estas proporciones como “dividir un segmento en media y extrema razón”.
Las maravillas de la razón áurea
Como escribió Mario Livio (Livio, 2002, pág. 6), “de hecho, probablemente la razón áurea ha inspirado a intelectuales de todas las ciencias como no lo ha hecho ningún otro número en la historia de las matemáticas”. Desde que los antiguos griegos descubrieron la razón áurea en los pentágonos y al dividir un segmento en media y extrema razón, su uso en el arte y en la arquitectura ha suscitado interés por su atractivo estético. Los tres volúmenes de la obra Divina Proportione, publicados por Luca Pacioli en 1509 y bellamente ilustrados por Leonardo da Vinci, impulsaron el uso de la razón áurea en el arte. En el siglo XX, en el libro Le Modulor, el arquitecto Le Corbusier presentó un sistema de proporciones basado en la razón áurea que aún continúa influyendo hoy día en arquitectos y artistas. Por último, las teselas de Roger Penrose, basadas en triángulos isósceles cuyos lados están en proporción áurea, nos han proporcionado nuevos resultados matemáticos en los que desempeña un papel importante este viejo número.
De la misma forma que \( \sqrt{2} \) es la longitud de la diagonal del cuadrado unidad, \( \varphi \) es la longitud de la diagonal de un pentágono regular de lado 1, como se ve en la Figura 2.4. (Véase el Desafío 2.4).
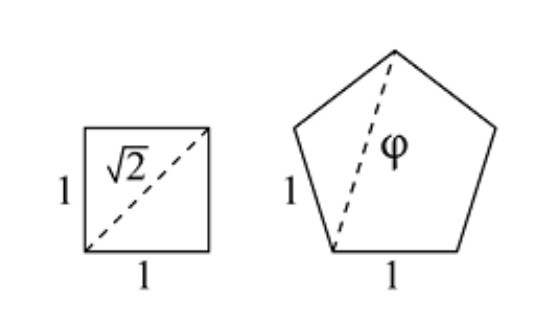
Como \( \varphi^2 = \varphi + 1 \), podemos escribir cualquier potencia entera positiva de \( \varphi \) en la forma \( a + b\varphi \), con \( a \) y \( b \) enteros. Para ello, comenzamos por multiplicar los dos miembros de la igualdad \( \varphi^2 = \varphi + 1 \) por \( \varphi \) y después seguimos repitiendo el proceso:
Para establecer el patrón que siguen \( a_n \) y \( b_n \), escribamos \( \varphi^n = a_n + b_n \varphi \) para \( n \ge 2 \), con \( a_1 = b_1 = 1 \). Entonces,
\[ \varphi^{n+1} = (a_n + b_n \varphi)\,\varphi = a_n\,\varphi + b_n\,\varphi^2 = a_n\,\varphi + b_n(\varphi + 1) = (a_n + b_n)\varphi + b_n. \]
de forma que \( a_{n+1} = b_n \), \( b_{n+1} = a_n + b_n \). La sucesión \( \{b_n\} \) es la sucesión \( \{F_n\} \) de los números de Fibonacci, ya que cumple la misma regla de recurrencia y tiene los mismos valores iniciales (véase el Apartado 1.6). Cambiando \( \{b_n\} \) por \( \{F_n\} \) nos queda que \( \varphi^n = F_{n-1} + F_n \varphi \), para \( n \ge 2 \).
Dado que \( \frac{1}{\varphi} = \varphi - 1 \), podemos establecer una relación similar para las potencias enteras negativas de \( \varphi \): \( (-1)^n \varphi^{-n} = F_{n-1} - F_n \varphi \). De aquí se deduce lo siguiente:
Así llegamos a la fórmula de Binet, que expresa los números de Fibonacci en términos de la razón áurea.
Teorema 2.3 (fórmula de Binet). \( F_n = \dfrac{\varphi^n - (-1)^n \varphi^{-n}}{\sqrt{5}}. \)
Dado que \( (-1)^n \varphi^{-n} = F_{n-1} - F_n \varphi \), se obtiene que el cociente de números de Fibonacci consecutivos tiene límite cuando \( n \to \infty \):
Haciendo crecer un rectángulo áureo
Consideremos un proceso iterativo de construcción de rectángulos: Una vez construido el enésimo rectángulo de la sucesión, el siguiente (el \( n+1 \)) es el rectángulo más pformulaueño que contiene dos copias adosadas del enésimo, una en posición horizontal y la otra en vertical. Si empezamos por un cuadrado de dimensiones \( 1\times 1 \), el proceso genera una sucesión de rectángulos cuyos lados son números de Fibonacci, como vemos en la Figura 2.5. Por tanto, los rectángulos de esta sucesión se van pareciendo cada vez más a un rectángulo áureo.
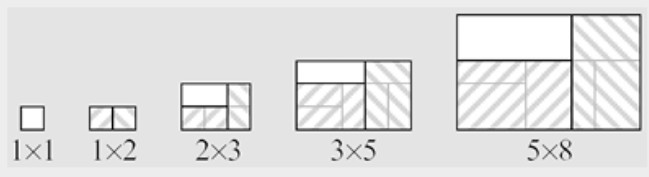
Si empezamos la sucesión con un rectángulo arbitrario, los rectángulos de la sucesión se van haciendo cada vez más “áureos” (Walser, 2001).
Dado que \( F_{n+1} = F_n + F_{n-1} \), podemos escribir \[ \frac{F_{n+1}}{F_n} = 1 + \frac{1}{F_n / F_{n-1}}, \] de forma que repitiendo el proceso (teniendo en cuenta que \( \frac{F_2}{F_1} = 1 \)) se obtiene que
y se llega a la expresión (con \( n - 2 \) signos “+”):
Tomando el límite y usando que \( \displaystyle \lim_{n\to\infty} \frac{F_{n+1}}{F_n} = \varphi \), se obtiene que
Dado que \[ \sqrt{k + \sqrt{k + \sqrt{k + \cdots}}} = \frac{1 + \sqrt{1 + 4k}}{2}, \] para \( k \ge 1 \) (véase el Desafío 2.16), también se cumple que
En la Figura 2.6 se ilustra cómo tiende esta expresión a \( \varphi \).
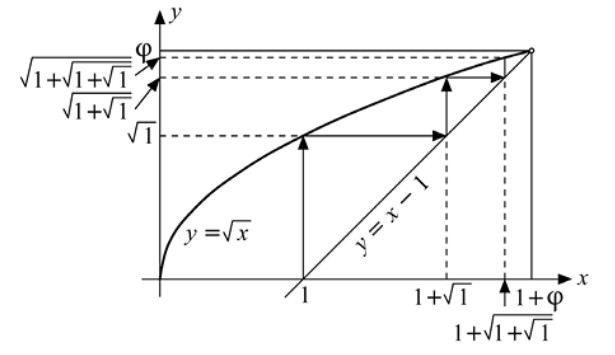
2.4. La circunferencia y \( \pi \)
El número \( \pi \) se define habitualmente como el cociente entre el perímetro y el diámetro de una circunferencia. Todos los estudiantes aprenden que la longitud de la circunferencia \( C \) es \( 2\pi r \) y el área \( A \) del círculo que encierra es \( \pi r^2 \), siendo \( r \) el radio de la circunferencia. ¿Por que aparece la misma constante \( \pi \) en ambas fórmulas? Una respuesta intuitiva bastante antigua es la que se ilustra en la Figura 2.7. Si cortamos un círculo de radio \( r \) en un número par grande de cuñas congruentes con forma de sector circular, podemos luego recolocarlas en una disposición que se asemeja a un rectángulo con base \( \pi r \) (media circunferencia) y altura \( r \), por ello \( A \) deberá ser \( \pi r^2 \).
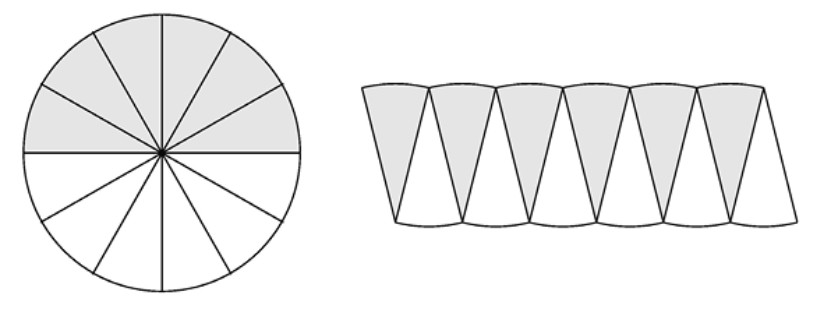
Naturalmente, este argumento no es una demostración, pero podemos formalizarlo con rigor usando límites. Para ello, circunscribimos polígonos regulares en el círculo y nos fijamos en que el área del polígono es igual a \( r \) veces su semiperímetro. Luego, tomamos el límite cuando el número de lados tiende a infinito. Puestos a utilizar límites, por el mismo precio podemos usar toda la potencia del cálculo, así que lo hacemos a continuación (Assmus, 1985). Usando integrales definidas para expresar el área y la longitud de arco, tenemos que
Mediante el cambio de variable \( x = r t \), se llega a
La cuestión ahora es la siguiente: ¿cómo comparar los dos integrales? Para ello, usamos la igualdad \( 1 = (1 - t^2) + t^2 \) e integramos por partes. Así, obtenemos que
Por tanto, como se cumple que
(la longitud de la semicircunferencia de radio 1), tenemos que \( A = \pi r^2 \).
2.5. La irracionalidad de \( \pi \)
Puede que no sirva para nada saber que \( \pi \) es irracional pero, si podemos saberlo, sería intolerable no hacerlo.
Edward Charles Titchmarsh
Teorema 2.4. \( \pi \) es irracional.
La elegante demostración de la irracionalidad de \( \pi \) que viene a continuación (Niven, 1947) usa solo cálculo elemental. Es todo un clásico.
Demostración: Supongamos que \( \pi = a/b \), siendo \( a \) y \( b \) enteros positivos. Para \( x \in [0,\pi] = [0,a/b] \), definimos los polinomios
y
donde especificaremos más adelante el valor del entero \( n \). Dado que todos los términos de \( x^k (a - bx)^n \) son de grado mayor o igual que \( n \), los valores de \( f(0) \) y \( f^{(n)}(0) \) son 0 para todos \( 0 \le k \le n - 1 \); y, como
tenemos que
es siempre un entero para \( n \le k \le 2n \). Lo mismo ocurre para \( x = \pi = a/b \), ya que \( f(\pi - x) = f(\pi - \pi) = 0 \).
Ahora tenemos que
Por tanto,
Ahora bien, \( F(\pi) + F(0) \) es un entero, ya que \( f^{(n)}(0) \) y \( f^{(n)}(\pi) \) lo son. Pero para \( x \in [0,\pi] \), \( f(x)\,\sin x > 0 \), y el valor máximo de \( f(x) \) es \( f(\tfrac{\pi}{2}) \), por lo que
de forma que la integral en (2.1) es positiva, pero con un valor tan cercano a 0 como queramos para \( n \) lo suficientemente grande. Concluimos, por tanto, que (2.1) es falso, así como la hipótesis de que \( \pi \) es racional. ■
El valor de \( \pi \) en la Biblia
Todos hemos oído que en alguna parte de la Biblia se afirma que el valor de \( \pi \) es 3. La fuente de esta afirmación es I Reyes 7.23 (también II Crónicas 4.2), donde la Biblia (New International Version) describe un redondo “mar” (un gran recipiente) hecho de metal, de diez codos de diámetro y treinta de circunferencia. El error de la aproximación es solo de un 4.5%. Un círculo de radio 1 tiene área \( \pi \), y el dodecágono inscrito tiene un área ligeramente menor, como vemos en la Figura 2.8. Si cortamos un cuarto del dodecágono en nueve piezas (tres triángulos formulauiláteros y seis triángulos isósceles con un ángulo de 150°) y las recolocamos (Kürschak, 1898), entonces es fácil ver que el área del dodecágono inscrito es exactamente 3, de forma que π se parece a 3 pero se pasa un poco.
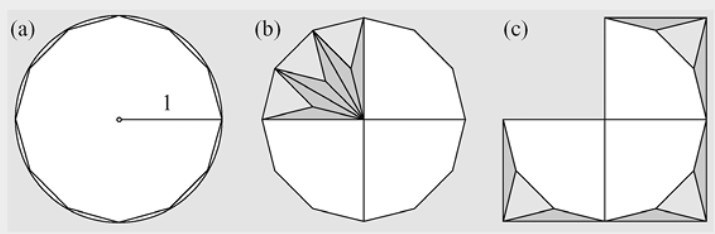
También es posible comparar el perímetro de la circunferencia con el de un hexágono regular inscrito y llegar a la misma conclusión.
2.6. El conde de Buffon y su aguja
En 1733, el naturalista, historiador y matemático francés Georges-Louis Leclerc, conde de Buffon (1707–1788), propuso el siguiente problema: si tiramos al azar una aguja sobre una mesa rayada con líneas paralelas formulauidistantes, ¿cuál es la probabilidad de que caiga sobre alguna de las rectas? Este problema es ahora conocido como el problema de la aguja de Buffon, y su solución (adaptada de Grinstead y Snell, 1997) proporciona un método probabilístico para hallar aproximaciones de \( \pi \). Supongamos que \( L \) es la longitud de la aguja, y que la distancia entre dos líneas de la mesa es \( D \), donde \( 0 < L \le D \). Véase la Figura 2.9a. Tenemos entonces el siguiente resultado.
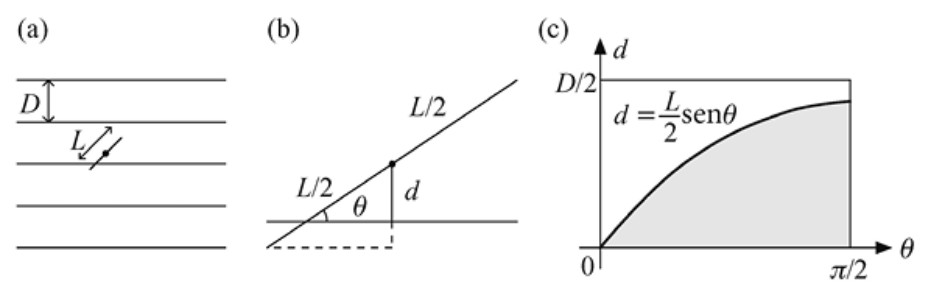
Teorema 2.5. Trazamos líneas paralelas, separadas entre sí una distancia \( D \), en una mesa. Dejamos caer una aguja de longitud \( L \) sobre la mesa (\( 0 < L \le D \)). La probabilidad de que la aguja corte a una de las líneas viene dada por \( p = \frac{2L}{\pi D} \).
Demostración. Llamemos \( d \) a la distancia del centro de la aguja a la línea más cercana y \( \theta \) al ángulo que forma la aguja con las líneas paralelas; así, \( d \) está en el intervalo \( [0, D/2] \) y \( \theta \in [0, \pi/2] \). Véase la Figura 2.9b. Entonces, la aguja corta una línea si y solo si \[ d \le \frac{L}{2}\,\sin\theta . \]
Suponiendo que los valores de \( \theta \) entre 0 y \( \pi/2 \) están uniformemente distribuidos, la probabilidad de que la aguja corte una línea será el cociente entre el área de la región sombreada de la Figura 2.9c y el área \( \pi D/4 \) del rectángulo que la encierra. El área de la región sombreada es
de ahí que \[ p = \frac{L/2}{\pi D / 4} = \frac{2L}{\pi D}. \] ■
Si escogemos \( L = D \), la probabilidad de cortar una línea es \( p = 2/\pi \). Ello nos sugiere un experimento para calcular \( \pi \): tirar una aguja de longitud unidad \( n \) veces sobre una mesa en la que se hayan trazado líneas paralelas a distancia 1 y contar el número de veces \( x \) que la aguja toca alguna línea. Entonces, el cociente \( 2n/x \) es una aproximación de \( \pi \). Hay que decir, sin embargo, que esta forma práctica de obtener una aproximación decente de \( \pi \) es pero que muy ineficiente: según nos dice un lanzamiento de la aguja para obtener la primera cifra correcta de \( \pi \) tiene solo una confianza del 95% (Gridgeman, 1960). La solución al problema de la aguja de Buffon es un ejemplo de probabilidad geométrica y fue un punto de partida para el estudio del campo donde confluyen la geometría y la probabilidad: la geometría integral.
2.7. El número \( e \) como límite
Hay varias formas de definir el número \( e \). Seguramente la más común sea como el límite
Para justificar esta definición, debemos asegurarnos de que el límite existe. Esto se hace habitualmente mostrando que la sucesión \[ \left\{ \left( 1 + \frac{1}{n} \right)^n \right\} \] es creciente y acotada, puesto que entonces será convergente y acotada tiene límite (resultado que no probaremos aquí).
La demostración que ofrecemos a continuación (Johnsonbaugh, 1974) es atractiva porque contiene un elemento visual y no hace uso de logaritmos. Probamos primero que para \( 0 \le a < b \) y cualquier entero positivo \( n \),
Esto se sigue del hecho de que la gráfica de \( y = x^{n+1} \) es convexa, de forma que la pendiente de una recta secante que une dos puntos de la gráfica es menor que la pendiente de la recta tangente en el punto de mayor abscisa. Véase la Figura 2.10.
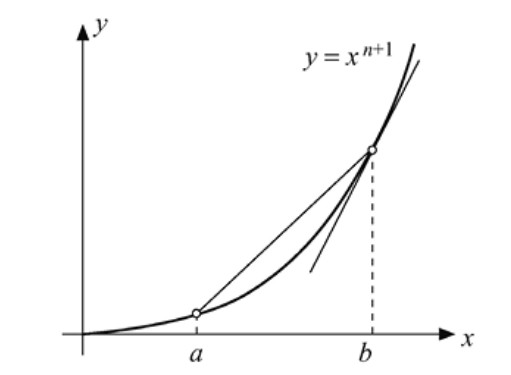
Si quitamos denominadores y reorganizamos los términos, (2.2) se convierte en
Tomando \( a = 1 + \frac{1}{n+1} \) y \( b = 1 + \frac{1}{n} \), el término del corchete de (2.3) se reduce a 1, y nos queda que
Si hubiéramos tomado \( a = 1 \) y \( b = 1 + 1/(2n) \), el corchete valdría \( 1/2 \) y tendríamos que
Multiplicando los términos de esta desigualdad por 2 y elevándolos al cuadrado, obtenemos que
Las desigualdades (2.4) y (2.5) implican que la sucesión \( \left\{ \left( 1 + \frac{1}{n} \right)^n \right\} \) es creciente y acotada superiormente, por tanto, tiene límite.
De igual forma, podemos probar que la sucesión \[ \left\{ \left( 1 + \frac{1}{n+1} \right)^{n+1} \right\} \] es decreciente, acotada inferiormente (véase el Desafío 2.11) y tiene el mismo límite que la anterior. Así, para \( n \ge 1 \),
Esta desigualdad puede ser mejorada sustancialmente reemplazando los exponentes \( n \) y \( n+1 \) por sus medias geométrica y aritmética, \( \sqrt{n(n+1)} \) y \( n + 1/2 \):
Para demostrar (2.7), probamos primero que, si \( a \) y \( b \) son dos números distintos positivos, su media logarítmica \( (b-a)/(\log b - \log a) \) está entre la media geométrica \( \sqrt{ab} \) y la aritmética \( (a+b)/2 \) (el hecho de que la media geométrica es menor o igual que la aritmética se demuestra fácilmente desarrollando y simplificando \( (\sqrt{b} - \sqrt{a})^2 \ge 0 \)).
Supongamos que \( 0 < a < b \). En la Figura 2.11a vemos que el área \( (b-a)/(\log b - \log a) \) bajo la gráfica de \( y = 1/x \) en el intervalo \([a,b]\) es mayor que el área \( 2(b-a)/(b+a) \) del trapecio sombreado, o lo que es lo mismo, \[ \frac{b-a}{\log b - \log a} < \frac{a + b}{2}. \] La Figura 2.11b muestra, a su vez, que el área \( (\log b - \log a) \) es menor que la suma de las áreas de los dos trapecios sombreados, que vale \( (b-a)/\sqrt{ab} \). Es decir, \[ \sqrt{ab} < \frac{b-a}{\log b - \log a}. \] Así, hemos establecido la doble desigualdad entre la media logarítmica y las medias geométrica y aritmética, para \( 0 < a < b \):
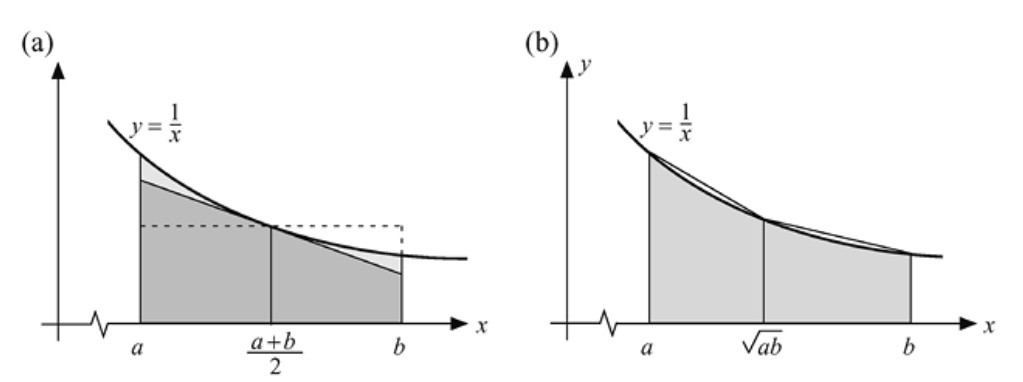
Tomemos ahora \( a = n \), \( b = n+1 \), e invertamos la desigualdad anterior para obtener
que es formulauivalente a (2.7). ¿Cuánto mejora la doble desigualdad (2.7) a la (2.6)? Para \( n = 50 \), la desigualdad (2.6) nos da \( 2{,}69159 < e < 2{,}74542 \); mientras que con (2.7) obtenemos \( 2{,}71824 < e < 2{,}71837 \). La anchura del segundo intervalo de acotación es inferior al 0,25 % de la del primer intervalo.
2.8. Una serie infinita para \( e \)
Mostramos a continuación que es posible expresar \( e \) como un límite diferente del anterior que, además, nos permite obtener una expresión en forma de serie infinita. Se suele obtener este límite usando polinomios de Taylor. Nosotros lo haremos utilizando integración por partes (Chamberland, 1999) para que aparezca la sucesión de las sumas parciales de la serie.
Teorema 2.6. \( e = \displaystyle \lim_{n\to\infty} \left( 1 + \frac{1}{n} + \frac{1}{2!n} + \cdots + \frac{1}{n!} \right) = 1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots \)
Demostración. Sea \( a_n = \frac{1}{n!} \int_{0}^{1} t^n e^{-t}\, dt \). Integrando por partes, encontramos que para \( n \ge 1 \) tenemos que
con \( a_0 = \frac{1}{e} \), de forma que
Dado que el integrando de la expresión que define \( a_n \) está acotado entre 0 y 1, se cumple entonces que \( 0 < a_n < 1 \), y por tanto, tenemos que
lo que nos permite escribir \( e \) como el límite que aparece en el enunciado del teorema. ■
2.9. La irracionalidad de \( e \)
Podemos ahora usar la serie obtenida en el apartado anterior para probar que \( e \) es irracional. La demostración que damos a continuación está tomada de (Hardy y Wright, 1960).
Teorema 2.7. El número \( e \) es irracional.
Demostración. Supongamos que \( e \) es racional, es decir, que es posible escribir \( e = p/q \) con \( p \) y \( q \) enteros positivos. Entonces,
Pasemos la primera suma a la derecha del primer término, y multipliquemos ambos miembros de la igualdad resultante por \( q! \). Así, obtenemos lo siguiente:
Pero el miembro izquierdo de (2.8) es un entero, mientras que el derecho es menor que 1, lo cual es imposible. Concluimos, por tanto, que \( e \) es irracional. ■
2.10. El problema de Steiner sobre el número \( e \)
En el clásico texto de Heinrich Dörrie, 100 Great Problems of Elementary Mathematics (Dörrie, 1965), se atribuyen ocho de ellos a Jakob Steiner (1796–1863). Este es el problema 89:
¿Para qué valor positivo de \( x \) alcanza su máximo la función \( x^{1/x} \)?
Un planteamiento habitual para este tipo de problemas consiste en usar métodos de cálculo para encontrar el máximo de la función \( f(x) = x^{1/x} \). Aquí damos una sencilla solución que hace uso solo de la convexidad de la función exponencial y la monotonicidad de la función potencial.
Solución: Probamos que para \( x \) positivo, \( x^{1/x} \le e^{1/e} \). Véase la Figura 2.12.
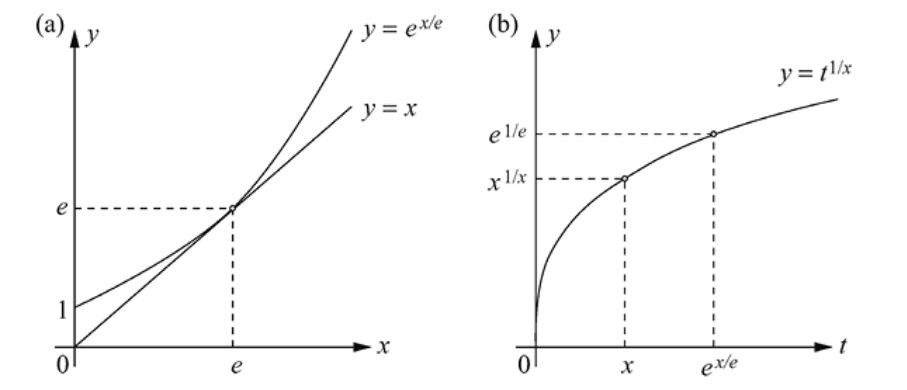
En la Figura 2.12a hemos dibujado la recta \( y = x \), tangente a la curva \( y = e^{x/e} \) en el punto \( (e,e) \). Entonces, para \( x > 0 \), se cumple que \( x \le e^{x/e} \). Elevando ambos miembros de esta desigualdad a la potencia \( 1/x \) (véase la Figura 2.12b para el caso \( x > 1 \)), obtenemos el resultado deseado (el caso \( x < 1 \) solo difiere en la concavidad).
En el Apartado 12.4 usaremos esta desigualdad para establecer la relación entre la media aritmética y la media geométrica para \( n \) números.
2.11. La constante de Euler–Mascheroni
La constante de Euler–Mascheroni \( \gamma \) mide cuánto difieren las sumas parciales de la serie armónica respecto del logaritmo natural. Para valores grandes de \( n \), la cantidad
Esta constante aparece en muchas áreas del análisis y la teoría de números, y volverá a aparecer más adelante cuando estudiemos sumas parciales, aproximaciones y estimaciones asintóticas.
Para probar que (2.9) tiene sentido, es decir, que ese límite existe, consideremos la sucesión
para \( n \ge 1 \), y veamos que es creciente y que está acotada superiormente. Tenemos
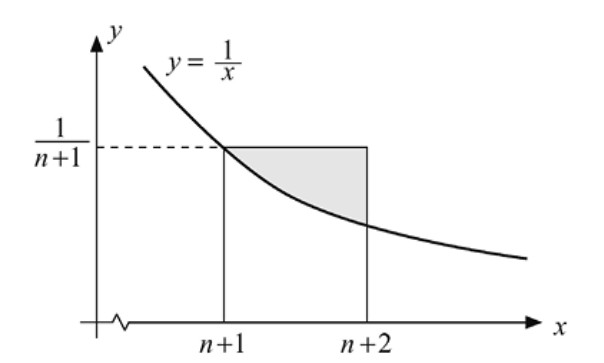
\[ a_{n+1} - a_n = \frac{1}{n+1} - \log(n+2) + \log(n+1) = \frac{1}{n+1} - \int_{n+1}^{n+2} \frac{1}{x}\, dx > 0, \]
como se ilustra en la Figura 2.13, donde la región sombreada representa la diferencia entre el área \( 1/(n+1) \) de un rectángulo cuya base es el intervalo \([n+1, n+2]\) y el área delimitada por la gráfica \( y = 1/x \) sobre el mismo intervalo.
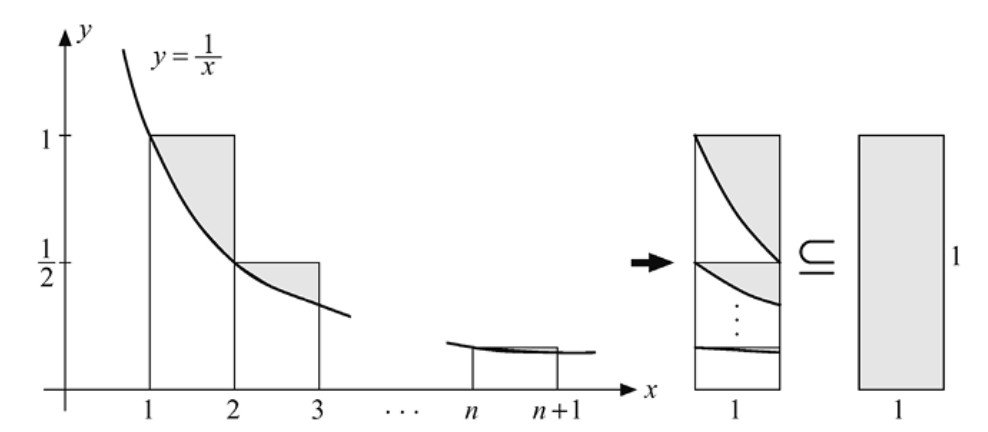
Además, \( a_n < 1 \) para todo \( n \), como se muestra en la Figura 2.14, donde se representa \( a_n \) mediante las n regiones sombreadas situadas por encima de la gráfica \( y = 1/x \) sobre el intervalo \([1, n+1]\). De aquí se deduce que el límite (2.9) existe. Su valor aproximado con veinte cifras decimales es \( \gamma \approx 0.57721566490153286060 \). Se desconoce todavía si es racional o irracional.
2.12. Exponentes, racionales e irracionales
Si dos números a y b son racionales, lo son también su suma y su producto. Si uno es racional y el otro irracional, la suma a + b o el producto a b son irracionales. Si ambos son irracionales, no podemos decir nada a priori.
¿Qué podemos afirmar acerca de la racionalidad o irracionalidad de \( a^b \) en función de cómo sean a y b? Si a y b son racionales, aⁿ es racional. Si a y b son irracionales, puede ser racional o irracional (\( 2^{\sqrt{2}} = 4^{1/2} = 4^{\sqrt{2}/2} \)). Algunas veces pueden ocurrir si a o b son irracionales (Jones y Toporowski, 1973).
Teorema 2.8. Una potencia irracional de un número racional puede ser un número racional.
Demostración: Para probar este teorema, necesitamos solo encontrar un ejemplo. Si \( \sqrt{2} \) fuera racional, ese sería nuestro ejemplo. Si \( \sqrt{2} \) no fuera racional, entonces nos serviría como ejemplo \( (\sqrt{2})^{\sqrt{2}} = 2 \). ■
Teorema 2.9. Una potencia irracional de un número irracional puede ser un número irracional.
Demostración: Si \( \sqrt{2} \) fuera irracional, ese sería nuestro ejemplo. En caso contrario, nos serviría como ejemplo \( \sqrt{2}^{\,\sqrt{2}+1} = \sqrt{2}^{\,\sqrt{2}} \cdot \sqrt{2} \). ■
Examinaremos los otros casos: las potencias irracionales de números racionales y las potencias racionales de números irracionales, en el Desafío 2.14.
Los lectores astutos se habrán dado cuenta de que hemos probado los Teoremas 2.8 y 2.9 sin decidir si \( \sqrt{2}^{\sqrt{2}} \) es racional o no. Solo hemos usado el hecho de que \( \sqrt{2} \) es irracional. De todas maneras, se sabe que \( 2^{\sqrt{2}} \) es irracional, dado que es la raíz cuadrada del número de Gelfand-Schneider \( 2^{\sqrt{2}} \), que es trascendente (un número trascendente no es algebraico, es decir, no es la raíz de un polinomio no nulo con coeficientes enteros; todos los números reales trascendentes son irracionales). Nadie sabe si \( \sqrt{2}^{\sqrt{2}} \) es racional o irracional.
Hilbert y el número de Gelfand-Schneider \(2^{\sqrt{2}}\)
El 8 de agosto de 1900, David Hilbert (1862-1943) presentó una ponencia en el Segundo Congreso Internacional de Matemáticas en París. En ella, Hilbert dio una lista de veintitrés problemas (en la versión impresa, aunque solo diez en la presentación oral) cuyas resoluciones, en su opinión, tendrían un impacto profundo en el desarrollo de la investigación matemática del siglo XX.
En el séptimo problema, Hilbert conjeturó que “la expresión \(a^{b}\), siendo la base \(a\) un número algebraico (distinto de 0 y de 1) y el exponente \(b\) un número algebraico irracional (por ejemplo, \(2^{\sqrt{2}}\) o \(e^{\pi} = i^{-2i}\)), siempre representa un número trascendente o, al menos, irracional”. La conjetura fue probada de forma independiente por A. O. Gelfand y T. Schneider en 1934.
Sin embargo, aún no se sabe si \(a^{b}\) es trascendente cuando los dos (\(a\) y \(b\)) son trascendentes.
2.13. Desafíos
- Encontrar demostraciones visuales como la de la Figura 2.1 para probar que (a) \( \sqrt{3} \) y (b) \( \sqrt{5} \) son irracionales.
- Demostrar que \( \sqrt{2} \) es irracional probando que la congruencia \( m^2 \formulauiv 2n^2 \pmod{3} \) no tiene soluciones si \( m \) y \( n \) son primos entre sí.
-
Probar que \( \sqrt{5} \) es irracional para \( n \ge 3 \).
[Indicación: usar el último teorema de Fermat: \( x^n + y^n = z^n \) no tiene soluciones enteras positivas para \( n \ge 3 \).] - Probar que la longitud de una diagonal de un pentágono regular de lado 1 es el número de oro.
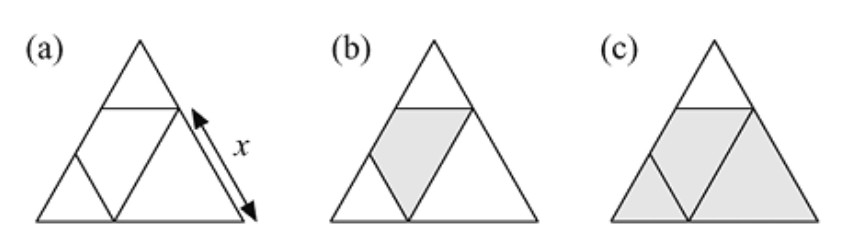
- Dividimos un triángulo formulauilátero de lado 1 en tres triángulos formulauiláteros y un trapecio por medio de líneas paralelas a sus lados, tal y como se ve en la Figura 2.15a. Probar que los trapecios sombreados en la Figura 2.15b y en la Figura 2.15c son semejantes y si y solo si se cumple que \( x = 1/\varphi \).
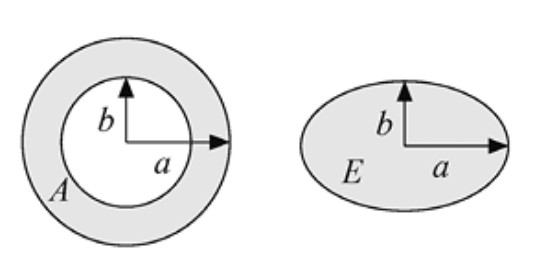
- Sea \( A \) el área de una corona circular de radio mayor \( a \) y radio menor \( b \), y sea \( E \) el área de una elipse cuyos semiejes son \( a \) y \( b \), como se muestra en la Figura 2.16. Hallar la razón entre \( a \) y \( b \) si las áreas \( A \) y \( E \) son iguales (Rawlins, 1995).
- Tres rectángulos idénticos de dimensiones \( a \times b \), con \( a < b \), se disponen como se muestra en la Figura 2.17a (perpendiculares dos a dos y con intersección común en el centro de los tres rectángulos). Sus vértices determinan entonces un poliedro convexo de caras triangulares (Figura 2.17b). Demostrar que el poliedro es un icosaedro regular y, si y solo si \( b/a = \varphi \), entonces los cinco rectángulos son secciones de un icosaedro regular.
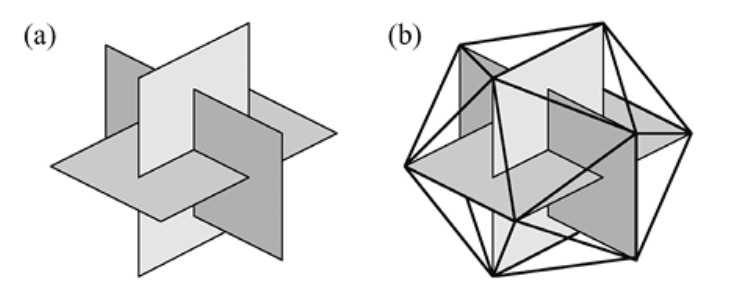
Figura 2.17.

2.8. Denotamos como ⟦x⟧ la función entero más próximo a x (si x es semientero, entonces ⟦x⟧ es el número par más próximo a x). Probar que para n ≥ 1, Fₙ = ⟦φⁿ/5⟧.
2.9. Una sucesión de la forma {a, b, a + b, a + 2b, 2a + 3b, …}, con a · b ≠ 0, en la que cada término a partir del segundo es la suma de los dos anteriores, es lo que se conoce como una sucesión generalizada de Fibonacci. ¿Hay alguna de ellas que sea a su vez una progresión geométrica?
2.10. Probar que π < 22/7. [Indicación: probar que 22/7 − π = ∫₀¹ x⁴·(1−x)⁴/(1+x²) dx.]
Este fue el problema A-1 en la vigesimonovena edición de la William Lowell Putnam Mathematical Competition en 1968.
2.11. (a) Probar que para 0 ≤ a < b y todo entero positivo n se cumple que
(b) Usar (a) para probar que
(c) Probar que las sucesiones
tienen igual límite y, por tanto,
2.12. Probar que
2.13. ¿Qué es mayor, eⁿ o nⁿ?
2.14.
(a) Mostrar que un número racional elevado a una potencia irracional puede ser irracional.
(b) Mostrar que un número racional elevado a una potencia irracional puede ser racional.
(c) ¿Por qué no preguntamos lo que pasa al elevar un número irracional a una potencia racional?
2.15. Si \( \{a_n\} \) es la sucesión de (2.10), probar que \( \gamma - a_n > \dfrac{1}{2(n+1)} \), lo que significa que la convergencia a 0 es muy lenta.
2.16. Mostrar que para \( k \ge 2 \), \[ \sqrt{k + \sqrt{k + \sqrt{k + \cdots}}} = \frac{1 + \sqrt{1 + 4k}}{2}. \]
[Indicación: considerar la sucesión definida por \( x_1 = \sqrt{k} \), \( x_{n+1} = \sqrt{k + x_n} \), y probar que es creciente y acotada superiormente].
Capítulo 3 — Puntos en el plano
Poderosa es la Geometría; unida al Arte, irresistible.
Eurípides
La Geometría es el arte de razonar bien sobre figuras mal hechas.
George Pólya
En este capítulo presentamos algunos resultados enigmáticos (y sus hermosas demostraciones) sobre algunas de las configuraciones geométricas más sencillas que podemos construir en el plano. Estas consisten solamente en puntos y rectas, que en muchos casos unen puntos de un retículo. En capítulos posteriores estudiaremos otros objetos geométricos como triángulos, cuadriláteros y círculos.
3.1. La fórmula de Pick
El teorema de Pick nos fascina por su elegancia y simplicidad; es una joya de la geometría elemental. Aunque fue probado por primera vez en 1899, no se le prestó mucha atención hasta setenta años después, cuando Hugo Steinhaus lo incluyó en la primera edición de su bello libro Mathematical Snapshots (Steinhaus, 1969). Georg Alexander Pick (1859–1924) nació en Viena, pero vivió muchos años en Praga. Pick escribió numerosos artículos matemáticos sobre ecuaciones diferenciales, análisis complejo y geometría diferencial. Tristemente, fue arrestado por los nazis en 1942 y enviado al campo de concentración de Terezín, donde murió.
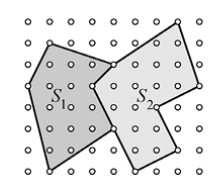
Un punto reticular o lattice point es un punto de coordenadas enteras y un polígono reticular es un polígono cuyos vértices son puntos reticulares. Decimos que un polígono es simple si sus lados no se cortan. El teorema de Pick expresa el área \(A(S)\) de un polígono reticular simple \(S\) en función del número de puntos reticulares que se encuentran en su interior \(I\) y del número de puntos reticulares que se encuentran sobre su perímetro \(B\): \(A(S) = I + pB/2 − 1\). Por ejemplo, para el polígono reticular \(S_2\) de la Figura 3.1, \(I_2 = 15\), \(p B_2 = 8\), y por tanto, \(A(S_2) = 18\).
Hoy en la enseñanza primaria los alumnos estudian a menudo el teorema de Pick. Usando un geoplano (una tabla con una disposición rectangular de clavos) y gomas elásticas, los estudiantes pueden construir polígonos y calcular sus áreas fácilmente.
Hay muchas formas de probar el teorema de Pick. Nuestra demostración (Varberg, 1985) es elegante por su simplicidad, además de directa e intuitiva. Hagamos primero notar que es posible dividir cualquier polígono reticular en triángulos reticulares (se puede probar esto fácilmente por inducción sobre el número de lados; basta con considerar una diagonal interior del polígono).
Comenzamos por definir el ángulo de visión \(\theta_q\) (en grados) para cada punto reticular \(P_q\) del polígono (interior o perimetral); es el ángulo con que \(P_q\) “ve” el interior del polígono y el peso del punto como \(\omega_q = \theta_q / 360^\circ\). Por ejemplo, \(\omega_q = 1\) para un punto reticular interior al polígono, \(\omega_q = 1/2\) para un punto reticular perimetral que no sea un vértice del polígono y \(\omega_q = 1/4\) para un vértice correspondiente a un ángulo interior recto. Sea \(W(S) = \sum_q \omega_q\), el peso total del polígono. Tenemos entonces el siguiente sorprendente resultado:
Lema 3.1. Si \(S\) es un polígono reticular simple, entonces \(W(S) = A(S)\).
Demostración. Al igual que sucede con el área, la función \(W\) es aditiva, es decir, si \(S_1\) y \(S_2\) son disjuntos (aunque puedan compartir, quizá, algún segmento del perímetro) y \(S = S_1 \cup S_2\) (véase el ejemplo de la Figura 3.1), entonces \(W(S) = W(S_1) + W(S_2)\). Esto se deduce de la observación de que los ángulos de visión en \(S_1\) y en \(S_2\), para un punto reticular común, se suman y dan el ángulo de visión en \(S\) para ese punto. Examinamos ahora varios casos.
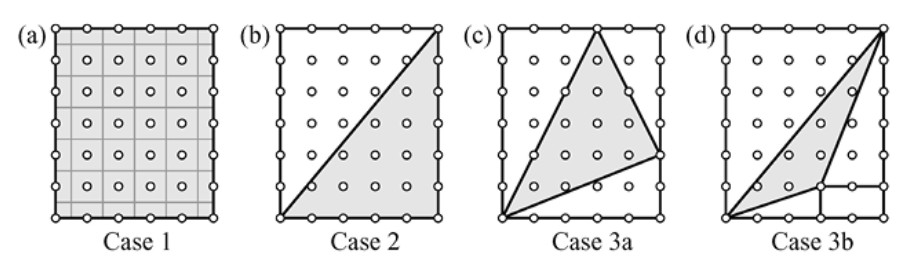
Caso 1. Consideremos un rectángulo reticular de lados horizontales y verticales, como el de la Figura 3.2a. Cada punto reticular se corresponde con uno y solo uno de los vértices de la cuadrícula (cuya área es igual al peso del polígono). Vemos así que el área del rectángulo de partida y su peso coinciden.
Caso 2. En la Figura 3.2b se muestra un triángulo rectángulo con un cateto horizontal y otro vertical. En este caso, \(W(S) = A(S)\), al ser \(S\) la mitad de un rectángulo como el del Caso 1 y ser \(W\) una función aditiva.
Caso 3. Juntando los casos anteriores, en las Figuras 3.2c y 3.2d, se muestra un triángulo rectángulo no recortado por triángulos como los del Caso 1 o rectángulos del Caso 2. De nuevo, \(W(S) = A(S)\) por la aditividad de \(W\).
Para completar la demostración para un polígono reticular simple arbitrario, basta con descomponerlo en unión de triángulos reticulares y usar la aditividad de \(W\).
Probamos ahora el teorema de Pick.
Teorema 3.1. Para un polígono reticular simple con \(i\) puntos reticulares interiores y \(p\) puntos reticulares perimetrales, se cumple que \(A(S) = i + p/2 - 1\).
Demostración. Si un polígono simple tiene vértices, entonces la suma de sus ángulos interiores es \((n - 2)\cdot 180^\circ\) (véase la prueba en el Apartado 4.1). Por ello, la suma de los ángulos de visión de todos los puntos reticulares perimetrales de \(S\) es \((p - 2)\cdot 180^\circ\). Si \(I\) y \(P\) son, respectivamente, el interior y el perímetro de \(S\), vemos entonces que
■
3.2. Circunferencias y sumas de dos cuadrados
El problema de representar un número como suma de dos cuadrados tiene una larga historia que se remonta, al menos, a la época de Pitágoras. Encontrar triángulos rectángulos con lados enteros es lo mismo que encontrar enteros positivos \(a\), \(b\) e \(c\), tales que \(c^2\) sea la suma de \(a^2\) y \(b^2\). De forma más general, podemos preguntarnos qué enteros \(n\) son suma de dos cuadrados y cuántas formas distintas hay de expresarlos de esa manera.
Sea \(r_2(n)\) el número de formas de representar \(n\) como la suma de dos cuadrados (de enteros positivos, negativos o de 0). Es decir, \(r_2(n)\) cuenta el número de parejas de enteros \((x,y)\) que son soluciones de la ecuación \(x^2 + y^2 = n\). Por ejemplo, \(r_2(5) = 8\), ya que las soluciones de \(x^2 + y^2 = 5\) son \((2,1)\), \((1,2)\), \((-1,2)\), \((-2,1)\), \((-2,-1)\), \((-1,-2)\), \((1,-2)\) y \((2,-1)\).
Dado que \(r_2(n) = 0\) cuando \(n\) es de la forma \(4k - 1\), el comportamiento de la función \(r_2\) es bastante irregular (véase el ejemplo de más abajo), pero nos preguntamos: ¿cuál es el promedio de \(r_2(k)\) para \(1 \le k \le n\)? Definamos \(N_2(n)\) como el número de soluciones enteras de la desigualdad \(x^2 + y^2 \le n\). Entonces, el promedio de los \(r_2(k)\) para \(1 \le k \le n\) es:
En la siguiente Tabla 3.1 podemos ver algunos valores de \(N_2(n)\) y \(N_2(n)/n\):
| n | 1 | 2 | 3 | 4 | 5 | 10 | 20 | 50 | 100 |
|---|---|---|---|---|---|---|---|---|---|
| \(N_2(n)\) | 5 | 9 | 9 | 13 | 21 | 37 | 69 | 161 | 317 |
| \(N_2(n)/n\) | 5 | 9/2 | 3 | 3.25 | 4.2 | 3.7 | 3.45 | 3.22 | 3.17 |
Tabla 3.1.
El valor medio de \(r_2\), para todos los enteros \(n\), es el límite de \(N_2(n)/n\) cuando \(n \to \infty\), si es que existe. Su valor viene dado en el siguiente teorema.
Teorema 3.2. \(\displaystyle \lim_{n\to\infty} \frac{N_2(n)}{n} = \pi.\)
Demostración. Está basada en la interpretación de \(N_2(n)\), y se debe a Carl Friedrich Gauss (1777–1855). El número \(N_2(n)\) es el número de puntos con coordenadas enteras situados en el interior de la circunferencia \(x^2 + y^2 = n\) o sobre ella. Por ejemplo, \(N_2(10) = 37\), ya que en el círculo centrado en el origen y de radio \(\sqrt{10}\) hay 37 puntos reticulares, como se ilustra en la Figura 3.3a.
Si dibujamos un cuadrado de lado 1 con centro en cada uno de los 37 puntos, entonces el área total de los cuadrados grises es de 37. Así que esperamos que la suma de las áreas de esos cuadrados se vaya aproximando cada vez más al área del círculo correspondiente, o lo que es lo mismo, que \(N_2(n)\) sea cada vez más parecido a \(\pi\!\left(\sqrt{n}\right)^{\!2}\).
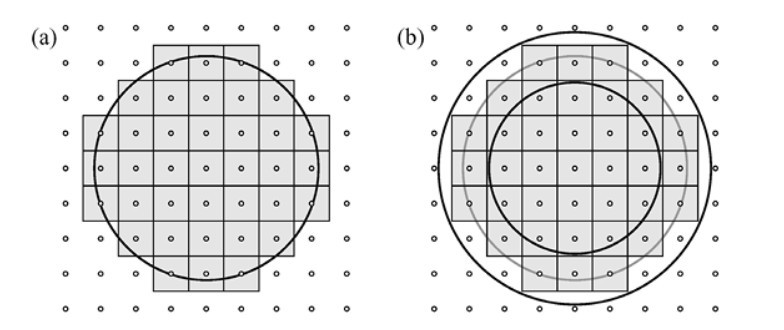
Si aumentamos el radio de la circunferencia en la mitad de la longitud de la diagonal de un cuadrado unidad hasta el valor de \(\sqrt{n} + \sqrt{2}/2\), entonces contendrá todos los cuadrados; mientras que si lo reducimos a \(\sqrt{n} - \sqrt{2}/2\) la circunferencia resultante estará contenida en la unión de los cuadrados. Por ello, el área de la unión de los cuadrados \(N_2(n)\) cumple que
3.3. El teorema de Sylvester–Gallai
En 1893, James Joseph Sylvester (1814–1897) propuso el siguiente problema en la columna de “Preguntas Matemáticas” del Educational Times:
Probar que no es posible colocar un número finito de puntos en el plano de forma que cualquier recta que pase por dos de ellos también pase por un tercer punto, a no ser que se encuentren todos sobre una recta.
Según parece, unos cuarenta años más tarde Tibor Gallai (1912–1992) lo resolvió, pero su prueba no fue publicada; de hecho, Paul Erdős propuso el siguiente problema en American Mathematical Monthly (Erdős, 1943):
Sean \(n\) puntos del plano que tengan la propiedad de que la recta que pasa por dos de ellos pasa también por un tercer punto. Probar que los \(n\) puntos están alineados.
Al parecer, Erdős desconocía tanto el problema propuesto por Sylvester como la solución de Gallai. Desde entonces han aparecido bastantes más demostraciones de lo que ahora conocemos como teorema de Sylvester–Gallai. La que damos a continuación, sencilla, directa y elegante, se debe a L. M. Kelly (Coxeter, 1948).
Teorema de Sylvester–Gallai 3.3. Si un número finito de puntos del plano no están en línea recta, entonces existe una recta que solo pasa por dos de ellos.
Demostración. Llamemos \(P\) al conjunto de puntos, y sea \(L\) el conjunto de rectas determinadas por los puntos de \(P\). Para cada punto \(p \in P\) y cada recta \(\ell \in L\) que tenga la propiedad de que \(p\) no está en \(\ell\), consideramos al par \((p, \ell)\) y calculamos la distancia de \(p\) a \(\ell\).
Dado que tanto \(P\) como \(L\) son conjuntos finitos, tenemos que considerar solo un número finito de parejas \((p, \ell)\). Por ello podemos encontrar un par \((p_0, \ell_0)\) para el cual la distancia es la mínima. Ahora probemos que \(\ell_0\) contiene solo dos puntos de \(P\).
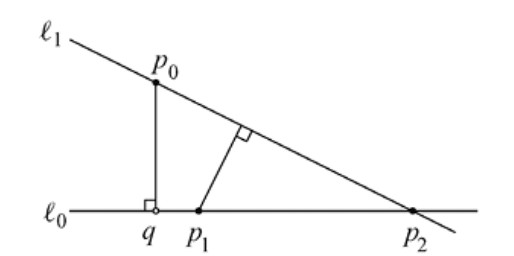
Supongamos que tuviera tres o más puntos de \(P\). Sea \(q\) (que puede o no ser un punto de \(P\)) el pie de la perpendicular a \(\ell_0\) trazada desde \(p_0\). De los puntos de \(P\) en \(\ell_0\), al menos dos de ellos deben estar en un mismo lado de \(q\). Sean estos \(p_1\) y \(p_2\), de forma que \(p_1\) (que puede coincidir con \(q\), esto es, \(p_1 = q\)) esté más cerca de \(p_0\) que \(p_2\). Sea \(\ell\) la recta de \(L\) determinada por \(p_0\) y \(p_1\).
Vemos que la distancia de \(p_2\) a \(\ell\) es menor que la distancia de \(p_0\) a \(\ell_0\). Pero esto contradice la elección del par \((p_0, \ell_0)\) como el que tenía la distancia mínima. Por tanto, \(\ell_0\) contiene exactamente dos puntos de \(P\). ■
3.4. Partiendo en dos un conjunto de cien mil puntos
Supongamos que seleccionamos cien mil puntos al azar dentro de un círculo. ¿Es siempre posible trazar una recta que divida al círculo en dos partes de forma que haya cincuenta mil puntos a cada lado de la recta? La respuesta es afirmativa (Gardner, 1989). De hecho, la respuesta es afirmativa para cualquier número \(2n\) de puntos situados en el interior del círculo. En la Figura 3.5 se muestra un procedimiento para hallar esa recta en un ejemplo con seis puntos. El método se puede extender de manera directa a cualquier número par de puntos.
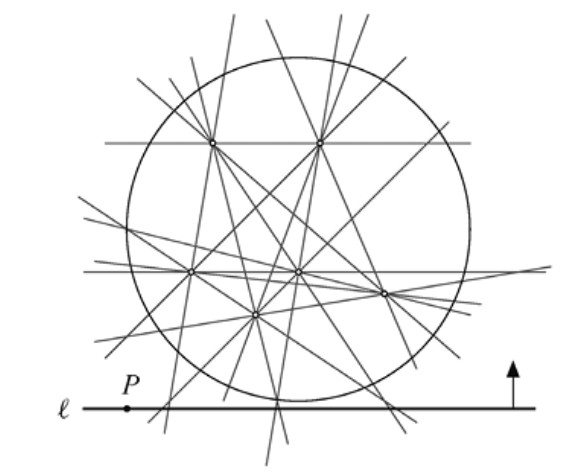
Consideremos todas las rectas determinadas por pares de puntos situados dentro del círculo y escojamos un punto \(P\) exterior al círculo que no se encuentre sobre ninguna de ellas. Dibujemos entonces una recta \(\ell\) que pase por \(P\) y que no corte al círculo, como se muestra en la Figura 3.5. Empecemos a rotar \(\ell\) alrededor de \(P\). Al hacerlo, pasará por cada uno de los puntos del interior del círculo de uno en uno, ya que \(P\) no se encuentra en ninguna de las rectas que unen dos o más puntos.
Habrá un momento en el que \(\ell\) habrá pasado exactamente por \(n\) puntos. En el giro hacia el punto \(n + 1\), y antes de llegar a él, pararemos. En ese momento quedarán \(n\) puntos en cada uno de los semiplanos determinados por la recta \(\ell\). ■
El principio del palomar, también conocido como principio de Dirichlet, es una herramienta simple pero poderosa para resolver problemas y probar teoremas. Fue enunciado por primera vez por Peter Gustav Lejeune Dirichlet (1805–1859) en 1834. Se basa en la elemental observación de que, si \(m\) palomas se distribuyen en \(n\) palomares y \(m > n\), entonces habrá un palomar que contenga al menos dos de las palomas. Por ejemplo, en la Figura 3.6 vemos diez palomas en nueve palomares.

Ross Honsberger (1973) cuenta la siguiente historia sobre Paul Erdős y Louis Pósa. Cuando Pósa tenía unos 11 años de edad, Erdős le planteó la siguiente cuestión mientras almorzaban: “Demuestra que, si tienes \(n + 1\) enteros positivos menores o iguales que \(2n\), debe haber al menos un par de ellos que sean primos entre sí”. Pósa respondió medio minuto después: “Si tienes \(n + 1\) enteros positivos menores o iguales que \(2n\), dos de ellos deben ser consecutivos y, por tanto, primos entre sí”.
Como se hace notar en Schattschneider (2006), este es el principio del palomar en su forma más pura: como “hay un máximo de \(n\) huecos no consecutivos en una hilera formada por \(2n\) de ellos, si intentamos colocar \(n + 1\) números en los \(2n\) huecos estaremos obligados a poner dos números (al menos) en huecos consecutivos”. En el Desafío 3.8 se plantea otro problema relacionado con los \(2n\) primeros positivos.
Presentamos ahora unos cuantos ejemplos adicionales —referidos a puntos del plano, o de una superficie o de una esfera— basados en este principio.
Ejemplo 3.1.
En cualquier conjunto de cinco puntos situados en el interior de un triángulo formulauilátero de lado unitario, existe al menos un par de ellos cuya distancia no es mayor que \(1/2\).
Para verlo, basta con dividir el triángulo en cuatro triángulos formulauiláteros iguales (cuatro palomares) de lado \(1/2\). Por el principio del palomar, al menos dos de los cinco puntos (palomas) estarán en el mismo triángulo pformulaueño.
Ejemplo 3.2.
(Problema A-2 de la 63rd William Lowell Putnam Mathematical Competition, 2002). Dados cinco puntos en una esfera, probar que al menos cuatro de ellos están en una misma semiesfera cerrada.
Dibujamos una circunferencia máxima (como el ecuador) que pase por dos de los puntos. Se forman así dos semiesferas cerradas que tienen esa circunferencia como frontera. Cada uno de los tres puntos restantes está en una de esas semiesferas, así que, según el principio del palomar, dos de esos puntos estarán en la misma semiesfera que la que contenía a los dos puntos iniciales.
En general, si se distribuyen \(m\) palomas en \(n\) palomares con \(m > n\), entonces al menos un palomar contendrá por lo menos \(\lceil m/n \rceil\) palomas, donde \(\lceil x \rceil\) representa la parte entera superior de \(x\) (el menor entero mayor o igual que \(x\)).
Ejemplo 3.3.
En cualquier conjunto de cincuenta y un puntos interiores de un cuadrado de lado unidad, hay siempre un subconjunto de tres puntos que pertenecen a un círculo de radio \(1/7\).
Ahora, dividimos el cuadrado en veinticinco cuadraditos de lado \(1/5\). Según el principio generalizado del palomar, debe haber un cuadrado pformulaueño que contenga \(\lceil 51/25 \rceil = 3\) puntos. Entonces, basta con darse cuenta de que, como \(\sqrt{2}/5 < 2/7\), cada cuadrado de lado \(1/5\) está dentro de un círculo cuyo centro coincide con el del cuadrado y que tiene un diámetro de \(2/7\).
A menudo es posible extender un principio de la matemática discreta para aplicarlo al caso continuo. Esto sucede con el principio del palomar. La dificultad principal estriba en decidir qué objetos son las palomas y cuáles son los palomares. Con frecuencia, en lugar de contar objetos, los medimos. He aquí un ejemplo (Strauss y Schinzel, 1999).
Ejemplo 3.4.
Si pintamos más de media esfera, siempre pintaremos al menos dos puntos antipodales.
Supongamos que no fuera así. Si reflejamos la esfera con respecto a su centro, la imagen de un punto pintado será otro punto no pintado. Entonces, la imagen \(N\) del conjunto \(P\) de puntos pintados será el conjunto de los puntos no pintados. De aquí se deduce que \(N\) y \(P\) son disjuntos y tienen igual área, lo cual es imposible ya que, por hipótesis, el área de \(P\) es mayor que la de media esfera. ■
3.6. Asignando números a puntos del plano
En el mes de abril de cada año, cerca de trescientas escuelas estadounidenses de enseñanza secundaria son invitadas a participar en la USAMO (United States of America Mathematical Olympiad), a la que pueden concurrir un puñado de seis problemas que hay que resolver en nueve horas durante dos días. El propósito de la USAMO es “detectar y estimular a los estudiantes líderes en matemáticas del país y señalar el talento en esa área”.
…más pueden ser resueltos sin usar cálculo, pueden constituir un desafío incluso para los matemáticos profesionales. Presentamos aquí el Problema 6 de la USAMO 2001 y la solución dada por uno de los participantes (Andreescu y Feng, 2002):
Problema 6.
A cada punto del plano se le asigna un número de manera que, para cualquier triángulo, el número asignado a su incentro es la media aritmética de los tres números asignados a sus vértices. Probar que se asigna el mismo número a todos los puntos del plano.
Solución.
(Michael Hamburg, St. Joseph’s High School, South Bend, Indiana). Se representa con una letra minúscula el número asignado al punto etiquetado con la correspondiente letra mayúscula. Sean \(A\) y \(B\) dos puntos arbitrarios. Consideremos el hexágono regular \(ABCDEF\) en el plano (véase la Figura 3.7). Sea \(G\) la intersección de las rectas \(CD\) y \(FE\) y la recta que pasa por \(G\) es perpendicular al segmento \(ED\).
Entonces, \(A, F, E\) y \(B, C, D\) son puntos respectivamente simétricos respecto a la recta \(E\). De aquí que los triángulos \(CEG\) y \(DFG\) compartan incentro, es decir, \(c + e = d + f\); además, los triángulos \(ACE\) y \(BDF\) también tienen el mismo incentro a \(+ c + e = b + d + f\). Por tanto, \(a = b\) y hemos acabado.
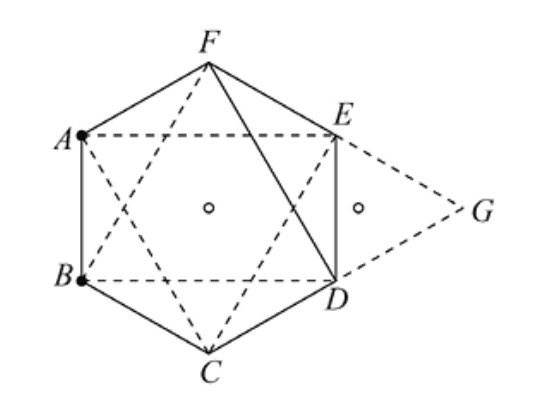
Cada año, el Clay Mathematics Institute (CMI) concede el premio Clay Olympiad Scholar a la solución que juzga más creativa. Hamburg recibió este galardón por su solución aportada en 2001. En su nota de prensa, el Clay Mathematics Institute decía lo siguiente:
“De los doce jueces de la USAMO Mathematical Olympiad Competition propusieron al Sr. Hamburg, estudiante de undécimo grado en la Saint Joseph’s High School, como el participante cuya respuesta a uno de los problemas de la prueba obedecía más a los criterios del CMI de elegancia, belleza, imaginación, profundidad y eficacia. El jurado de la misión que examinaba al Sr. Hamburg por su solución al Problema 6 de la prueba, que solo nueve de los doscientos setenta participantes en la ronda final resolvieron correctamente. Michel destacó una demostración particularmente ingeniosa y de forma concisa y adecuada. Universalmente, los jueces consideraron que su solución ofrecía una auténtica ‘demostración en palabras’”.
3.7. Desafíos
- ¿Es posible construir un triángulo formulauilátero reticular?
-
¿Existe alguna versión tridimensional del teorema de Pick para poliedros?
[Indicación: considerar un tetraedro de vértices (0, 0, 0), (1, 0, 0), (0, 1, 0) y (1, 1, k), siendo k un número entero positivo]. - ¿Por qué el teorema de Sylvester–Gallai no funciona para conjuntos infinitos de puntos?
-
Dados \(n \ge 3\) puntos no alineados del plano, el teorema de Sylvester–Gallai nos dice que debe haber una recta que solo contenga dos puntos. En realidad, hay más de una recta. De hecho, Kelly y Moser (1958) han probado que hay al menos \(3n/7\) rectas que solo contienen dos puntos. Probar que existe una distribución de puntos no alineados en el plano para la que hay exactamente \(3n/7\) rectas que solo pasan por dos puntos (y por ello la cota inferior de \(3n/7\) no puede ser mejorada).
[Indicación: n = 7]. - Considerar una parrilla rectangular de puntos reticulares con \(m\) puntos en cada una de sus \(n\) filas. Encontrar el número de rectángulos con vértices en los puntos reticulares y lados paralelos a los lados de la parrilla.
- Probar que, si \(n = 4k - 1\), para un entero k, entonces \(r_2(n) = 0\).
- Para cada entero positivo \(n\), sea \(N_3(n)\) el número de ternas \((x, y, z)\) de enteros tales que \(x^2 + y^2 + z^2 = n\). Probar que \(N_3(n)\) es aproximadamente \(4\pi n^{1/2} / 3\), para \(n\) lo suficientemente grande.
- Cada uno de los vértices de un pentágono regular se colorea de blanco o de negro (se usan los dos colores). Probar que hay tres vértices del mismo color que definen un triángulo isósceles.
- Probar que, si elegimos \(n + 1\) números entre los \(2n\) primeros enteros positivos, al menos dos de ellos cumplen que uno divide al otro.
-
(a) Pintemos todos los puntos del plano con dos colores distintos. Probar que hay cuatro puntos del mismo color que distan exactamente una pulgada.
(b) Pintamos todos los puntos del plano con dos colores distintos. Probar que hay dos puntos del mismo color que distan exactamente dos pulgadas.
(c) ¿Es cierta la afirmación del apartado (b) si cambiamos tres por nueve? - Pintamos todos los puntos del plano de rojo o azul. Probar que algún rectángulo tiene sus cuatro vértices del mismo color.
Capítulo 4 — El patio de los polígonos
Justo por encima se encuentra la Nobleza, en sus distintos grados, que empieza por las figuras de seis lados, o Hexágonos. A partir de ahí, los que tienen más lados reciben el honorable título de Polígonos, los de muchos lados.
Edwin A. Abbott, Flatland
Los polígonos, junto con las rectas y las circunferencias, fueron las primeras figuras geométricas estudiadas por los seres humanos. Los polígonos y las estrellas poligonales asociadas aparecen frecuentemente en la historia en forma de símbolos, a menudo en contextos religiosos y místicos. El libro IV de los Elementos de Euclides se ocupa exclusivamente de la construcción de algunos polígonos regulares (triángulos, cuadrados, pentágonos, hexágonos y pentadecágonos) y de cómo inscribirlos o circunscribirlos en circunferencias.
En este capítulo consideramos algunos resultados y demostraciones notables sobre polígonos generales. En capítulos posteriores estudiaremos polígonos particulares como los triángulos, cuadrados, cuadriláteros u otros polígonos que recubren el plano.
4.1. Combinatoria poligonal
Por polígono entendemos una figura cerrada con un número n finito de lados rectos (\(n \ge 3\)). Los polígonos pueden ser convexos, cóncavos o estrellados (véase la Figura 4.1). En ocasiones usaremos la palabra n-gono para referirnos a un polígono con n lados (y n ángulos).
(i) La suma de sus ángulos es \((n-2)\cdot 180^\circ\);
(ii) Hay \(n\cdot(n-3)/2\) diagonales;
(iii) Las diagonales se cortan, como mucho, en \(\binom{n}{4}\) puntos interiores.
Demostración.
Como el \(n\)-gono es convexo, podemos escoger un vértice y trazar las \(n-3\) diagonales que lo conectan con todos los demás que no sean sus vecinos. Las \(n-3\) diagonales dividen al \(n\)-gono en \(n-2\) triángulos; por tanto, la suma de los ángulos interiores es \((n-2)\cdot 180^\circ\). Para probar (ii), basta con darse cuenta de que de cada vértice salen \(n-3\) diagonales y cada diagonal une dos vértices, por tanto, el número de diagonales es \(n\cdot(n-3)/2\). Finalmente, para demostrar (iii), observemos que cada punto interior de intersección de diagonales también es punto de intersección de las dos diagonales de un cuadrilátero cuyos vértices lo son asimismo del polígono (véase Figura 4.2). Por consiguiente, el número de puntos de intersección es igual al número de formas de elegir cuatro vértices del \(n\)-gono, que es \(\binom{n}{4}\).
Ahora, consideramos un \(n\)-gono y todas sus diagonales. ¿Cuántos triángulos podemos encontrar en esa figura? Responderemos a esta pregunta en el caso de que no haya tres diagonales que se encuentren en el mismo punto, como sucede en el ejemplo de la Figura 4.2.
Teorema 4.2.
Sea \(P\) un \(n\)-gono convexo en el que no haya tres diagonales que se corten en un mismo punto interior. Entonces, el número de triángulos contenidos en \(P\) cuyos vértices son vértices de \(P\) o puntos de intersección de dos diagonales de \(P\) es
Demostración.
(Conway y Guy, 1996). Contamos los triángulos según el número de vértices que compartan con \(P\). Hay \(\binom{n}{3}\) triángulos cuyos tres vértices son vértices de \(P\) (véase la Figura 4.3a), \(4\binom{n}{4}\) triángulos que comparten dos vértices con \(P\) (véase la Figura 4.3b), \(5\binom{n}{5}\) triángulos que comparten solo un vértice con \(P\) (véase la Figura 4.3c) y finalmente \(\binom{n}{6}\) triángulos que son interiores a \(P\). ■
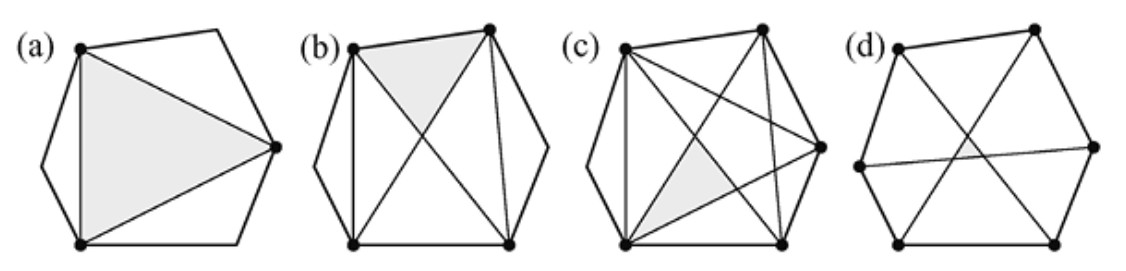
Una pregunta parecida es la siguiente: ¿en cuántas regiones queda dividido un polígono al trazar sus diagonales?
Teorema 4.3.
Sea \(P\) un \(n\)-gono convexo que no tenga tres diagonales que se corten en un mismo punto interior. Entonces, el número de regiones en las que queda dividido por sus diagonales es
Demostración.
(Honsberger, 1973; Freeman, 1976). Aquí vamos a usar el argumento de la línea giratoria del Apartado 3.4. Dado que \(P\) tiene un número finito de lados y diagonales, podemos seleccionar un punto \(Q\) exterior a \(P\) que no pertenezca a ninguna recta que sea la prolongación de una diagonal o un lado de \(P\) (véase la Figura 4.4).
Dibujamos una recta \(\ell\) que pase por \(Q\) y que no corte a \(P\), y la hacemos rotar alrededor de \(Q\). Contamos el número de regiones de \(P\) delimitadas por sus diagonales, contando una región cuando la recta móvil \(\ell\) la toca por primera vez en su rotación. Ello ocurre siempre en un vértice, que puede ser un vértice de \(P\) o un punto de intersección interior de dos diagonales.
Consideremos un punto de intersección interior \(I\). Antes de que \(\ell\) pase por \(I\), habrá cortado a tres de las cuatro regiones que tienen a \(I\) como vértice. Estas regiones habrán sido contadas antes, de forma que al pasar la recta \(\ell\) por \(I\) solo se encuentra una (y solo una) región nueva. Vemos así que el número de regiones contadas aumenta en una unidad cada vez que \(\ell\) toca a un punto interior \(I\).
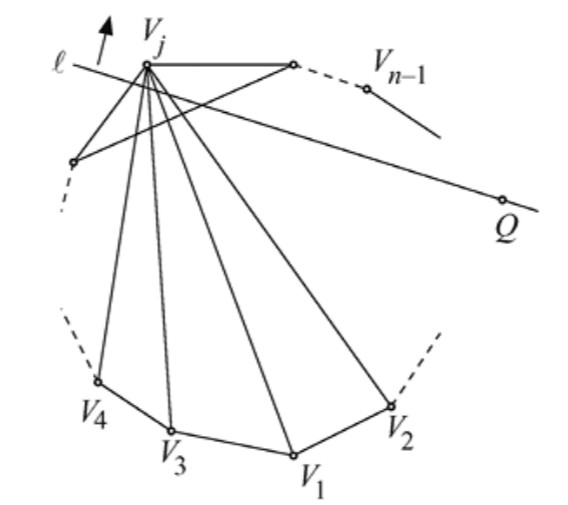
Consideremos ahora los vértices de \(P\). Cada vértice de \(P\) es un vértice que pertenece a \(n-2\) regiones triangulares. Nombremos los vértices en el orden en que son alcanzados por \(\ell\) en su rotación alrededor de \(Q\): \(V_1, V_2, \dots, V_m\). Inmediatamente después de pasar por \(V_i\), la recta \(\ell\) corta a los \(n-2\) triángulos formados por las diagonales que parten de \(V_i\), de modo que el número de regiones contadas aumenta en \(n-2\). Cuando \(\ell\) pasa por \(V_i\), el contador de regiones aumenta en \(n-3\), ya que un triángulo (el que comparte vértice \(V_i\)) ya había sido contado antes. Cuando pasa por \(V_m\), aumenta en \(n-4\), y así sucesivamente hasta llegar a \(V_1\). Es el momento en el que ya no quedan triángulos que contar.
Dado que en la rotación obtenemos una región más por cada punto de intersección interior, \(n-1\) regiones para cada \(V_j\) (con \(j = 1,2,\dots,n-1\)) y ninguna región para \(V_m\), el número total es
4.2. Dibujar un polígono conocidas las longitudes de sus lados
Es fácil dibujar un triángulo con lados de longitudes conocidas \(a, b, c\). ¿Qué pasaría si nos dieran las longitudes \(a_1, a_2, \dots, a_n\) de los lados de un \(n\)-gono (en un orden fijo)? ¿Podemos dibujar la figura, aunque no conozcamos los ángulos? La sorprendente respuesta es afirmativa.
Como podéis sospechar, nos hará falta usar algunas herramientas suplementarias además de las clásicas griegas: el compás y la regla. Necesitamos también una gran cartulina y tijeras. Se empieza por dibujar un arco de circunferencia grande en la cartulina. A partir de un punto cercano a uno de los extremos del arco, se construyen sobre él cuerdas de longitud \(a_1, a_2, \dots, a_n\) en la dirección del otro extremo. Así obtenemos una lista de puntos \(A_0, A_1, \dots, A_n\). Después unimos con la regla radios que vayan desde el centro de la circunferencia hasta los vértices de la poligonal. Recortando la figura y doblando por las líneas de los radios, se puede construir una pirámide cuya base será el \(n\)-gono buscado.
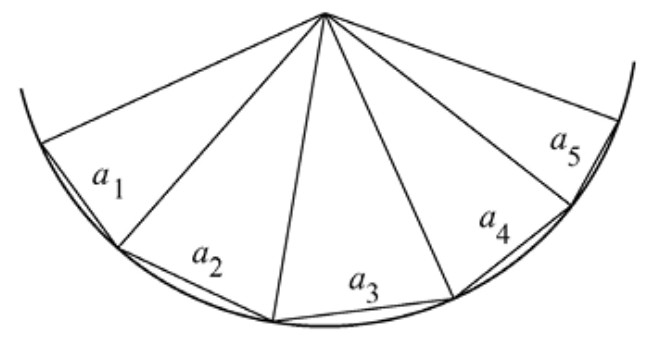
La paciencia y el 65 537-gono
La inscripción de polígonos regulares en una circunferencia usando regla y compás aparece por primera vez en el libro IV de los Elementos de Euclides. Allí se construyen el triángulo formulauilátero, el cuadrado y los polígonos regulares de cinco, seis y siete lados. Carl Friedrich Gauss (con 19 años de edad) demostró que el 17-gono regular podía ser construido con regla y compás, aunque no proporcionó su construcción explícita. El 257-gono regular fue construido en 1832 por Friedrich Julius Richelot (1808–1875) y el 65 537-gono regular lo fue por Johann Gustav Hermes (1846–1912) en 1894, después de diez años de total dedicación y duro trabajo. Esto muestra que la paciencia y la perseverancia son buenos complementos del talento matemático.
4.3. Los teoremas de Maekawa y Kawasaki
El origami (del japonés oru, ‘doblar’, y kami, ‘papel’) es el arte tradicional japonés de plegar una hoja de papel, normalmente cuadrada, con el fin de representar objetos como pájaros o flores. El origami plano es el que da lugar a figuras que pueden ser aplastadas sobre el plano sin que se produzcan nuevas dobleces o arrugas. Cuando desdoblamos una pieza de origami, el diagrama al que dan lugar los pliegues en el papel recibe el nombre de patrón de plegado. En un patrón de plegado tenemos dos tipos de pliegues, que reciben el nombre de pliegue-montaña y pliegue-valle (véase la Figura 4.6).
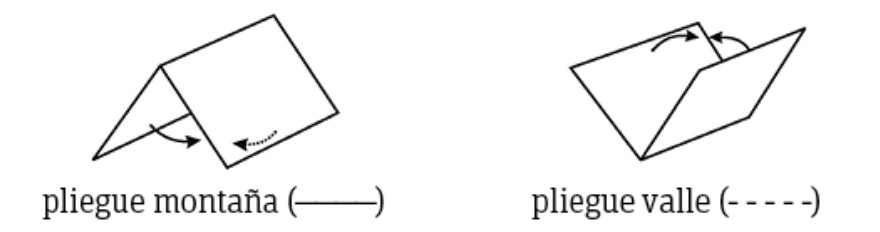
Señalamos con líneas continuas los pliegues-montaña y los pliegues-valle con líneas discontinuas. Un vértice de un patrón de plegado es un punto de intersección de dos o más líneas de pliegue. En un pliegado plano de un vértice es un patrón de plegado plano con un solo vértice. En la Figura 4.7 vemos una grulla de origami y una reproducción parcial de su patrón de plegado.
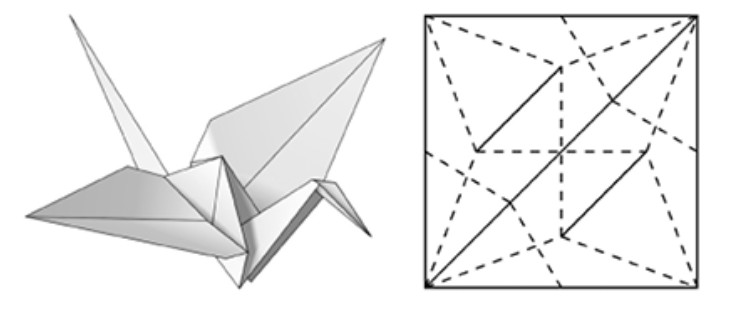
Vamos a ver ahora dos teoremas sobre plegados planos de un vértice y sus demostraciones. El primero se conoce con el nombre del físico japonés Jun Maekawa. Apareció publicado con este nombre en 1987, pero sin demostración. El matemático francés Jacques Justin lo había publicado, también sin demostración, en 1986. La sencilla prueba que damos a continuación fue encontrada por Jan Siwanowicz cuando era estudiante de bachillerato (Hull, 1994).
Teorema de Maekawa 4.4.
La diferencia entre el número de pliegues-montaña y el número de pliegues-valle en un plegado plano de un vértice es de 2.
Demostración.
Sea \(n\) el número de pliegues que confluyen en el vértice, m de los cuales son montañas y v son valles, de forma que \(n = m + v\). Cogemos el patrón de plegado del vértice. Doblamos el papel por los pliegues del vértice (véanse las Figuras 4.8a y 4.8b), y entonces, situando el vértice en la parte superior, damos un corte para obtener una sección poligonal plegada como la que se muestra en la Figura 4.8. Esta sección es un polígono aplastado, cuyos ángulos interiores son, o bien \(0^\circ\), o bien \(360^\circ\).
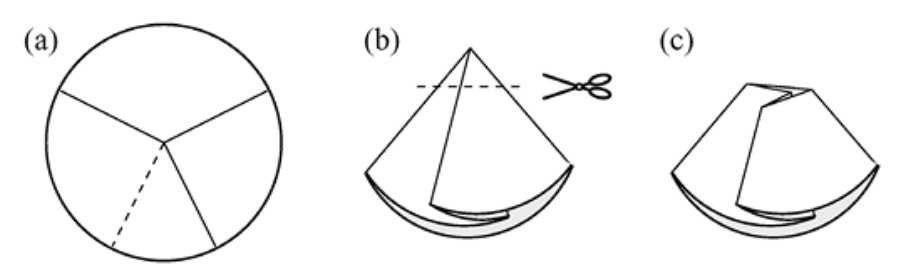
Mirando al polígono aplastado desde arriba, los pliegues-montaña se corresponden con los ángulos de \(0^\circ\) y los pliegues-valle con los de \(360^\circ\), por lo que la suma de los ángulos interiores es \(m\cdot 0^\circ + v\cdot 360^\circ\). Por otro lado, el Teorema 4.1(i) nos dice que en un polígono simple se cumple también \((n-2)\cdot 180^\circ = (m + v - 2)\cdot 180^\circ\), luego \(m\cdot 0^\circ + v\cdot 360^\circ = (m + v - 2)\cdot 180^\circ\). Si miramos el polígono desde abajo, los pliegues-montaña pasan a ser pliegues-valle, y viceversa; luego en ese caso \(m\cdot 360^\circ + v\cdot 0^\circ = (m + v - 2)\cdot 180^\circ\). Lo correcto es afirmar que \(|m - v| = 2\).
Dado que \(m\) y \(v\) difieren en dos, ambos deben ser pares o ambos impares, luego \(n = m + v\) es par. Lo que prueba el siguiente:
Corolario 4.1.
El número de pliegues que salen del vértice de un plegado plano de un vértice es par.
Como consecuencia, el número de ángulos entre los sucesivos pliegues es par. El siguiente teorema nos habla de la suma de los ángulos en un plegado plano de un solo vértice.
Teorema de Kawasaki 4.5.
La suma de ángulos alternos en un plegado plano de un vértice es de \(180^\circ\).
Demostración.
Sean \(\theta_1, \theta_2, \theta_3, \ldots, \theta_n\) los ángulos que coinciden en el vértice tomados por orden. Su suma es \(\theta_1 + \theta_2 + \theta_3 + \cdots + \theta_n = 360^\circ\). Si aplastamos el modelo de papel como en la Figura 4.8b y lo recorremos en un camino que vaya alrededor del vértice en el mismo orden de los pliegues, vemos que cada vez que encontramos un pliegue-valle aparece el simétrico de nuestro rectángulo.
Tras \(2n\) pasos, regresamos al punto de partida, así que también se cumple que \(\theta_1 - \theta_2 + \theta_3 - \cdots + (-1)^{n}\theta_n = 0\). Sumando las dos expresiones anteriores miembro a miembro, obtenemos \[ \theta_1 + \theta_3 + \theta_5 + \cdots = 180^\circ, \] y restándolas y dividiendo por 2, \[ \theta_2 + \theta_4 + \theta_6 + \cdots = 180^\circ. \]
El recíproco del teorema de Kawasaki es también cierto (véase Hull, 1994), pero pospondremos su demostración hasta más adelante (véase el Desafío 4.4).
Hay que tener en cuenta que los resultados que hemos presentado se aplican solo a plegados planos de un vértice; su extensión a plegados con más de un vértice es difícil.
4.4. Cuadratura de polígonos
Para los antiguos geómetras griegos, llevar a cabo la cuadratura de una figura significaba construir, en un número finito de pasos y usando solamente regla y compás, un cuadrado que tuviera igual área que dicha figura. Durante siglos, la cuadratura de figuras delimitadas por curvas (como círculos y lunas) ha atraído el interés matemático, pero el hecho de que cualquier polígono pueda ser “cuadrado” es bien conocido ya desde la Antigüedad. Por este motivo, no deja de causar cierta sorpresa que sea imposible conseguir la cuadratura del círculo pese a que podamos ver en cierto sentido en el límite que una sucesión de polígonos (todos ellos “cuadrables”). Tras probar un sencillo lema sobre la cuadratura de triángulos, presentamos dos teoremas que nos proporcionan métodos para cuadrar un polígono, el primero directo y el segundo inductivo.
Lema 4.1. Podemos lograr la cuadratura de cualquier triángulo utilizando regla y compás.
Demostración.
Introduzcamos el triángulo en un rectángulo tal y como se muestra en el primer diagrama de la Figura 4.9. Usando la construcción geométrica de la media geométrica \(\sqrt{a\cdot b}\) de dos números positivos \(a\) y \(b\), podemos entonces construir un cuadrado que tenga la misma área que el rectángulo. Uniendo los puntos medios de sus dos lados obtenemos el cuadrado buscado (véase la Figura 4.9).
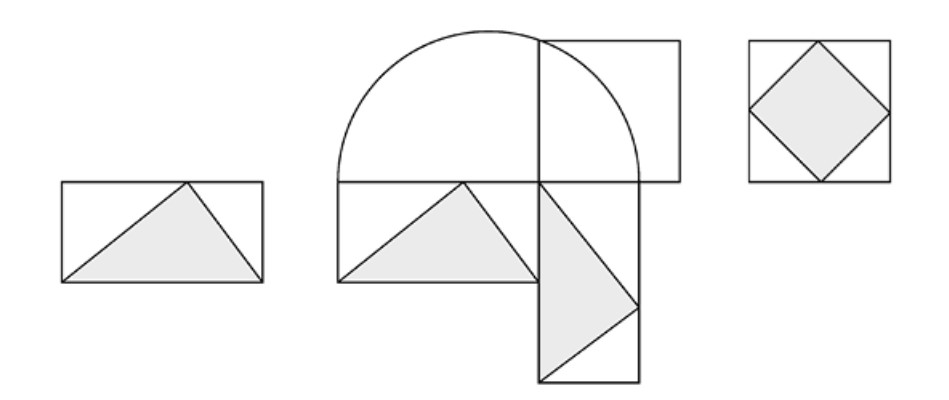
Teorema 4.6. Podemos lograr la cuadratura de cualquier n-gono convexo con regla y compás.
Demostración.
Si \(n = 3\), aplicamos el Lema 4.1. Para \(n \ge 4\), descomponemos el polígono en \(n - 2\) triángulos trazando las diagonales desde un vértice y aplicamos el Lema 4.1 a cada triángulo. De este modo, obtenemos \(n - 2\) cuadrados. Para construir un cuadrado cuya área sea la suma de las áreas de los cuadrados anteriores tomamos dos de ellos, los unimos por un vértice de manera que se forme un ángulo recto y construimos un cuadrado sobre el segmento que une los vértices que quedan a uno de los lados de las diagonales de los dos cuadrados que hemos unido. Repetimos el procedimiento con el cuadrado resultante y otro de los \(n - 2\) de partida hasta que no quede ninguno. ■
Teorema 4.7.
Dado un \(n\)-gono convexo \(P_n\), \(n \ge 4\), existe un \((n - 1)\)-gono convexo \(P_{n-1}\), de igual área, que puede ser construido a partir de \(P_n\) con regla y compás.
Demostración.
Véase la Figura 4.10. ■
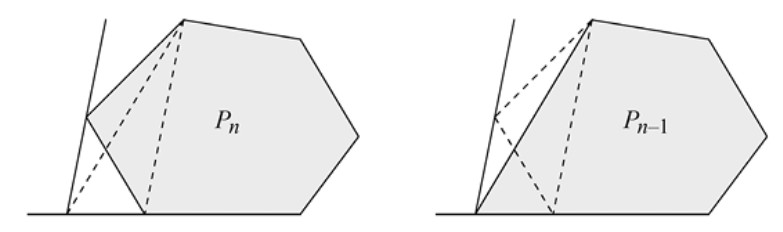
En el Capítulo 9 estudiaremos la cuadratura de figuras delimitadas por curvas.
4.5. Las estrellas del patio de los polígonos
Los polígonos convexos (y cóncavos) son simples en el sentido de que sus lados no se cortan. Cuando permitimos intersecciones de los lados, obtenemos polígonos estrellados. Etiquetamos los polígonos estrellados regulares con el símbolo \(p/q\), donde \(p\) y \(q\) son dos enteros positivos que cumplen la condición \(1 \le q < p/2\). El polígono estrellado regular \(p/q\) se construye conectando \(p\) puntos distribuidos uniformemente sobre una circunferencia (que borraremos posteriormente), de manera que \(q\) es el orden. En la Figura 4.11 tenemos, de izquierda a derecha, los polígonos estrellados \(\{5/2\}\), \(\{6/2\}\), \(\{7/2\}\), \(\{7/3\}\), \(\{8/2\}\) y \(\{8/3\}\).

Muchos polígonos estrellados regulares tienen nombre: \(\{5/2\}\) es el pentagrama; \(\{6/2\}\) es el hexagrama, estrella de David o sello de Salomón; \(\{8/2\}\) es la estrella de Lakshmi y \(\{8/3\}\) es el octagrama. El pentagrama ha sido usado como símbolo religioso pagano desde hace más de cinco mil años y también en los albores del cristianismo y en el islam. El pentagrama aparece en las banderas de Marruecos y Etiopía; la estrella de David en la bandera nacional de Israel y en la bandera de la Nigeria Británica anterior a su independencia en 1960. El octagrama aparecía en la bandera de la República de Irak entre 1959 y 1963.
Los polígonos estrellados aparecen con frecuencia como motivos geométricos en el arte islámico. En la parte izquierda de la Figura 4.12 podemos ver una estrella de tipo \(\{8/2\}\) de la decoración cerámica del patio del cuarto dorado de la Alhambra de Granada, construida con teselas en el siglo XIV. En el mosaico del centro, como se encuentra en los Reales Alcázares de Sevilla (siglo XIV), vemos una estrella \(\{8/3\}\), dentro de otra estrella \(\{8/2\}\), rodeada, a su vez, por otras ocho estrellas de tipo \(\{8/3\}\). En el mosaico de la derecha, también de los Reales Alcázares, se muestra una estrella \(\{12/4\}\) rodeada por estrellas \(\{6/2\}\) y \(\{8/2\}\).

Para pentágonos estrellados (no necesariamente regulares), tenemos el siguiente teorema. Su demostración se basa en la de (Nakhli, 1986).
Teorema 4.8.
Los ángulos de los vértices de cualquier pentágono estrellado suman \(180^\circ\).
Demostración.
Véase la Figura 4.13. ■
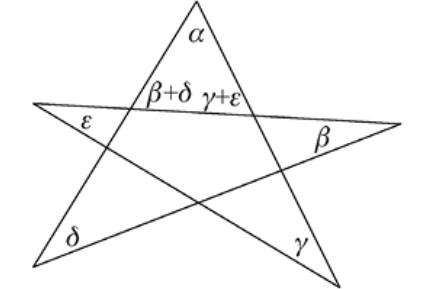
Los ángulos de los vértices de la estrella de David suman \(360^\circ\), ya que es la unión de dos triángulos formulauiláteros. En general, la suma de los ángulos de los vértices del polígono...
Si consideramos todos los posibles pentágonos (permitiendo intersecciones de los lados y ángulos de más de \(180^\circ\)), ¿cuántas clases de pentágonos hay? Siguiendo a (Steinitz, 1922), decimos que dos \(n\)-gonos propios y ordinarios, \(P_0 = [a_0, a_1, \dots, a_n]\) y \(P_1 = [b_0, b_1, \dots, b_n]\), son formulauivalentes si existe una familia uniparamétrica de \(n\)-gonos propios y ordinarios \(P(t) = [x_0(t), x_1(t), \dots, x_n(t)]\), con \(0 \le t \le 1\), para la que se cumple que \(P(0) = P_0\), \(P(1) = P_1\) (sea \(P_1\) o una imagen especular de él) y las funciones \(x_0(t), x_1(t), \dots, x_n(t)\) están contenidas en \([0,1]\). Con esta definición de formulauivalencia existen exactamente once clases de pentágonos (Grünbaum, 1975) que se muestran en la Figura 4.14.
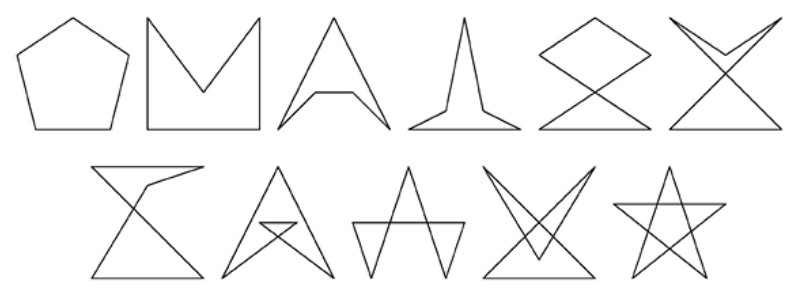
No se conoce aún la clasificación completa de los hexágonos, pero se han identificado setenta y dos clases distintas (Grünbaum, 1975).
Polígonos estrellados y estrellas poligonales
Un conjunto estrellado es un conjunto \(S\) de puntos con la propiedad de que existe un punto \(A\in S\) tal que, para cualquier otro punto \(X\in S\), el segmento \(AX\) está contenido en \(S\). Cuando \(S\) es un conjunto estrellado poligonal, lo llamamos estrella poligonal.
Aunque todo polígono estrellado es una estrella poligonal, no toda estrella poligonal es un polígono estrellado (por ejemplo, los polígonos convexos). Las estrellas poligonales se usan en el estudio de los problemas de visibilidad (véase el apartado siguiente) y en robótica.
4.6. Los vigilantes de la galería de arte
En 1973, Victor Klee formuló el famoso problema de las galerías de arte (Aigner y Ziegler, 2001): ¿cuántos vigilantes necesitamos en una galería de arte para asegurar que, entre todos ellos, mirando en todas las direcciones, pueden ver todos los puntos de la galería?
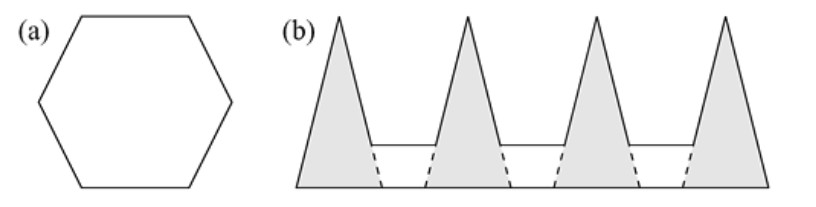
Consideremos el caso de una galería de arte poligonal. Cuando el polígono es convexo, nos basta claramente con un solo vigilante (véase la Figura 4.15a). Sin embargo, para polígonos cóncavos se puede necesitar más de uno. En la Figura 4.15b vemos una galería con forma de peine y doce paredes que rformulauiere cuatro vigilantes, cada uno situado en uno de los cuatro triángulos sombreados para poder observar cada uno de los dientes del peine.
La situación más general aparece reflejada en el siguiente teorema, demostrado por primera vez en (Chvátal, 1975). Nuestra demostración (Do, 2004) se basa en la elegante prueba de una página que aparece en (Fisk, 1978).
Teorema 4.9.
Para cualquier galería de arte poligonal con \(n\) paredes, son suficientes \(\lfloor n/3 \rfloor\) vigilantes, que pueden llegar a ser necesarios.
Demostración.
Que la condición es necesaria se demuestra con galerías en la forma de peine y dientes, como la de la Figura 4.15b. Estas tienen \(3k\) paredes y rformulauieren \(k\) vigilantes. Mediante un pformulaueño truncamiento de una o dos de las esquinas, obtenemos galerías con \(3k + 1\) o \(3k + 2\) paredes para las que también son necesarios \(k\) vigilantes.
Dividimos la demostración de que bastan \(\lfloor n/3 \rfloor\) vigilantes en tres pasos principales:
(i) Siempre podemos triangular un polígono. La triangulación de un polígono consiste en dividirlo en triángulos, que no se superpongan, mediante diagonales que unan pares de vértices y no se corten entre sí. Para justificar que eso es siempre posible, hay que mostrar que para todo polígono existe siempre una diagonal que une dos vértices y está contenida enteramente en él. En ese caso descomponemos esa diagonal para cortar el polígono en dos más pformulaueños, y repetimos con ellos hasta que solo queden triángulos.
Para ver que tal diagonal existe para \(n \ge 4\), colocamos un vigilante en el vértice \(A\) con un rayo láser apuntando al vértice contiguo \(B\). Si el vigilante ve el rayo hacia el interior del polígono, deberá acabar iluminando un tercer vértice \(C\) del polígono. En ese instante, podemos mover \(A\) o \(BC\) como la diagonal buscada siempre que no haya otro vértice del triángulo \(ABC\). Pero si ese vértice no existe, el rayo lo habría alcanzado antes de iluminar \(C\). ■
…que es cierto para \(m\)-gonos con \(3 \le m \le n\). Según el paso (i), para un \((n+1)\)-gono podemos encontrar una diagonal interior que nos permita dividirlo en dos más pformulaueños \(P\) y \(Q\) que, por hipótesis, podemos 3-colorar. Nos fijamos ahora en los colores de los dos vértices situados en los extremos de la diagonal en el polígono \(P\) y permutamos los colores en la 3-coloración de \(Q\) hasta que coincidan con los colores de los vértices de \(P\) (véase la Figura 4.16). Una vez hecho esto, volvemos a pegar los polígonos \(P\) y \(Q\) a lo largo de \(\ell\). Así, hemos obtenido una 3-coloración del \((n+1)\)-gono.
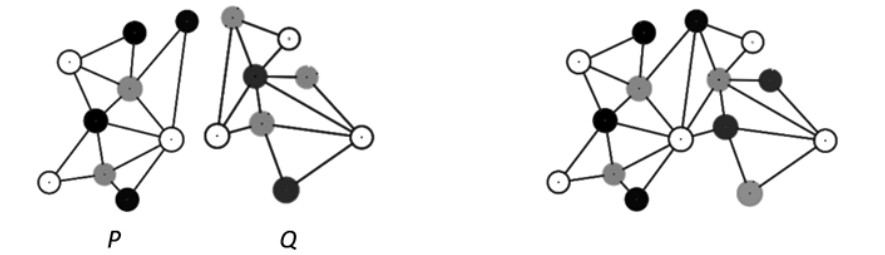
(iii) Coloquemos ahora vigilantes en los vértices pintados con el color menos usado.
Supongamos que los colores en los vértices son rojo, azul y amarillo. Si colocamos vigilantes en
todos los vértices de un mismo color, la galería estará totalmente vigilada. Así que escogemos el
color que aparezca menos veces (supongamos que es el rojo). Entonces, si el rojo aparece \(k\) veces
en la 3-coloración, se tiene que \(k \le n/3\), por como se es entero, \(k = \lfloor n/3 \rfloor\). ■
4.7. Triangulaciones de polígonos convexos
El problema de contar todas las posibles triangulaciones de un \(n\)-gono convexo dado tiene una historia distinguida. Fue enunciado por Leonard Euler (1707–1783) en una carta a Christian Goldbach (1690–1764) (Euler, 1965). Euler también propuso el problema a Jan Andrej Segner (1704–1777), que fue quien lo resolvió, aunque el propio Euler había sugerido soluciones para ciertos valores de \(n\). Más tarde fue propuesto como problema abierto por Joseph Liouville (1809–1894) y resuelto por diferentes matemáticos, entre ellos Gabriel Lamé (1795–1870). En este apartado presentaremos su argumento combinatorio (Lamé, 1838).
Como ejemplo, en la Figura 4.17 mostramos las triangulaciones de un cuadrado, de un pentágono y de un hexágono que en total son dos, cinco y catorce, respectivamente.
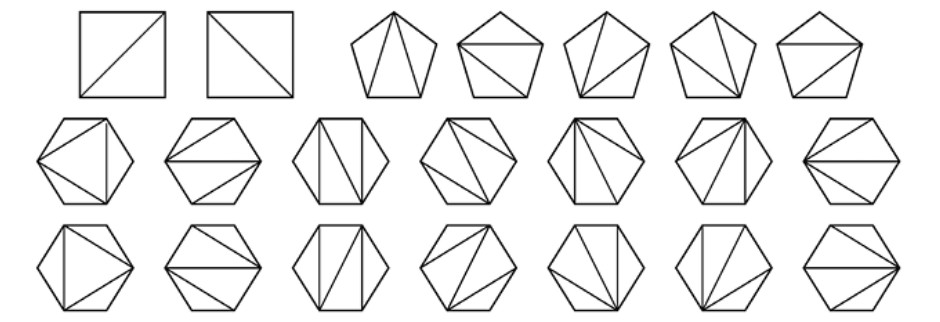
Teorema 4.10.
Sea \(T_n\), con \(n \ge 3\), el número de triangulaciones de un \(n\)-gono convexo. Entonces, \(T_3 = 1\) y, además:
(i) \(T_{n+1} = T_n + T_3 T_{n-1} + T_4 T_{n-2} + \dots + T_{n-2} T_4 + T_{n-1} T_3 + T_n,\quad n \ge 3.\)
(ii) \(T_n = n · (T_3 T_{n-1} + T_4 T_{n-2} + \dots + T_{n-2} T_4 + T_{n-1} T_3)/(2n - 6),\quad\) para \(n \ge 4\).
(iii) \(T_{n+1} = (4n - 6)\, T_n / n,\quad\) para \(n \ge 3\).
Demostración.
(i) Ilustramos el procedimiento que vamos a seguir con un octógono, pero está claro cómo extender el método a un \(n\)-gono. Véase la Figura 4.18.

Consideremos el lado inferior del octógono. Tras la triangulación, esta es la base de cada uno de los seis triángulos que se muestran en la figura. En cada uno de estos casos quedan por triangular un polígono (que puede ser un segmento o “2-gono”) que está situado a la derecha del triángulo y otro polígono que se encuentra a su izquierda.
En el primer octógono de la Figura 4.18 hay un segmento a la izquierda y un heptágono a la derecha, que puede ser triangulado de \(T_7\) formas. En el segundo octógono hay un triángulo a la izquierda y un hexágono a la derecha, que pueden ser triangulados en conjunto de \(T_3 \cdot T_6\) formas. Continuando de esta manera con los siguientes octógonos, se obtiene finalmente:
(ii) Para ilustrar la demostración, utilizamos como ejemplo un heptágono, pero es posible generalizarla a un \(n\)-gono (véase la Figura 4.19). Cada diagonal aparece en muchas triangulaciones. La diagonal situada más a la izquierda en la Figura 4.19 aparece en \(T_7 \cdot T_6\) triangulaciones, ya que divide al heptágono en un triángulo y un hexágono.
La diagonal que se encuentra a su derecha aparece en \(T_4 \cdot T_5\) triangulaciones, pues divide al heptágono en un cuadrilátero y un pentágono. Como el heptágono tiene siete vértices, el número \(L_7 = 7 \cdot (T_3 T_6 + T_4 T_5 + T_5 T_4 + T_6 T_3)\) cuenta todas las triangulaciones posibles obtenidas trazando diagonales que no se cortan, pero naturalmente algunas de ellas han sido contadas varias veces. En general, tenemos:
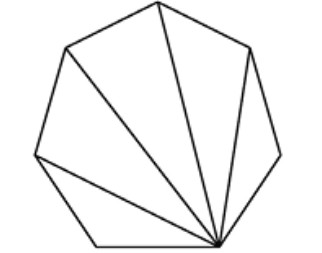
Cada triangulación de un \(n\)-gono tiene \(n - 3\) diagonales diferentes, y cualquier conjunto de \(n - 3\) diagonales aparecerá en la suma \(L_n\) exactamente \(2(n-3)\) veces, ya que toda diagonal tiene dos vértices. De este modo, concluimos que \(T_n = L_n/(2n - 6)\), como habíamos afirmado en el enunciado. Por último, (iii) es consecuencia inmediata de (i) y (ii). ■
El resultado (iii) del Teorema 4.10 proporciona una fórmula explícita para \(T_n\), que damos en el Corolario 4.2. Omitimos la demostración, que se obtiene por inducción matemática.
Corolario 4.2.
Sea \(T_n\) el número de triangulaciones de un \(n\)-gono convexo. Entonces,
Números de Catalan
Los números \(\{T_n\}_{n \ge 3}\), más conocidos como números de Catalan \(C_{n-2} = T_n\), es decir, el enésimo número de Catalan es el número de formas de triangular un \((n+2)\)-gono convexo \((n \ge 1)\).
También aparecen como soluciones de numerosos problemas de combinatoria, tales como contar las formas de colocar paréntesis en un producto, los caminos en una retícula cuadrada que no cortan a la diagonal o el número de árboles binarios. Reciben este nombre en honor a Eugène Charles Catalan (1814–1894), matemático francés nacido en Brujas (cuando aún formaba parte de Francia), que trabajó en teoría de números (en particular en fracciones continuas), geometría descriptiva y combinatoria. También se debe a él lo que se conoce como la conjetura de Catalan, que afirma que 8 y 9 son las únicas potencias perfectas consecutivas no triviales (la primera demostración de este resultado fue publicada en 2004 por Preda Mihăilescu).
4.8. Cicloides, ciclogónos y cicloides poligonales
Es bien sabido que cuando se hace rodar un círculo a lo largo de una recta, la curva generada por un punto de su circunferencia es una cicloide. Dos de las propiedades más bonitas de una cicloide son: (i) El área delimitada por un arco de la cicloide y la recta es tres veces el área del círculo generador. (ii) La longitud de un arco de cicloide es cuatro veces el diámetro de la circunferencia generadora. Puede que nos parezca sorprendente que se obtengan resultados parecidos si reemplazamos la circunferencia por un polígono regular.
Si en lugar de hacer rodar un círculo rodamos un polígono regular, la curva generada por uno de sus vértices está compuesta por arcos de circunferencias. A esta curva la conoce a veces como ciclogón (Apostol y Mnatsakanian, 1999). Véase la Figura 4.20a para el caso de un hexágono que rueda a lo largo de una recta.
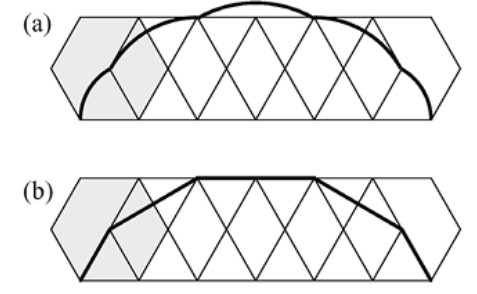
Si reemplazamos los arcos por sus cuerdas, la figura resultante recibe el nombre de cicloide poligonal. En el caso de un hexágono, se ilustra en la Figura 4.20b.
Vamos ahora a hallar el área situada bajo el arco de una cicloide poligonal y su longitud. Antes probaremos un lema que tiene interés por sí mismo.
Lema 4.2.
Sean \(V_1, V_2, V_3, \dots, V_n\) los vértices de un \(n\)-gono regular. Sea \(R\) la distancia de estos al centro del polígono y sea \(P\) cualquier punto de la circunferencia circunscrita al \(n\)-gono. Entonces,
Demostración.
(Ouellette y Bennett, 1979). Coloquemos el \(n\)-gono en el plano \(XY\) de forma que su centro coincida con el origen de coordenadas, y sean \(V_i = (a_i, b_i)\), \(P = (u, v)\). Entonces,
dado que \((u^2 + v^2) = (a_i^2 + b_i^2) = R^2\). Para completar la demostración basta con constatar que \(\sum a_i = \sum b_i = 0\). Para ello, coloquemos pesos iguales en los vértices del \(n\)-gono. Dado que el centro de gravedad de los \(n\) pesos será su centro, los momentos \(x\) e \(y\) del sistema serán nulos.
De aquí que \(\sum a_i = \sum b_i = 0\). (Se puede encontrar una demostración formal de este resultado utilizando números complejos en (Ouellette y Bennett, 1979)). ■
El caso en el que el punto \(P\) es uno de los vértices del polígono, que recogemos en el siguiente corolario, es especialmente interesante.
Corolario 4.3.
La suma de los cuadrados de las distancias de un vértice de un \(n\)-gono regular que dista \(R\) de su centro a los otros vértices es \(2nR^2\).
Probemos ahora que la propiedad del área de las cicloides mencionada anteriormente es cierta también para las cicloides poligonales.
Teorema 4.11.
Cuando un polígono regular rueda a lo largo de una recta, el área de la cicloide poligonal generada por un vértice del polígono es tres veces el área del polígono.
Demostración.
Sea \(R\) el radio de la circunferencia circunscrita al \(n\)-gono, y sean \(d_1, d_2, d_3, \dots, d_{n-1}\), las distancias de un vértice dado del \(n\)-gono (digamos \(V_1\)) a los otros \(n-1\) vértices (véase la Figura 4.21a).
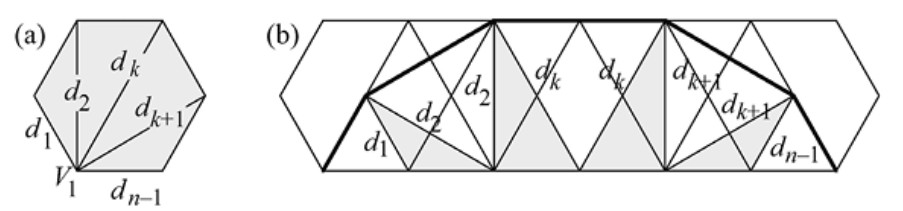
Sea \(A\) el área del \(n\)-gono regular con \(R = 1\). La Figura 4.21b muestra la cicloide poligonal generada por \(V_1\), cuando el polígono rueda sobre la recta. La región situada debajo de la cicloide poligonal puede ser dividida en \(n - 2\) triángulos sombreados y en \(n - 1\) triángulos isósceles, cada uno de ellos con un ángulo \(2\pi/n\) en el ápice. Los lados iguales de los triángulos isósceles miden \(d_1, d_2, \dots, d_{n-1}\) y así sucesivamente.
Los \(n - 2\) triángulos sombreados son congruentes, respectivamente, con los \(n - 2\) triángulos formados por las diagonales que parten de \(V_1\) en el \(n\)-gono de partida, por tanto, sus áreas suman \(A R^2\). Usando el Corolario 4.3, vemos que la suma de las áreas de los \(n - 1\) triángulos isósceles es
Por tanto, el área de la cicloide poligonal es \(3AR^2\), es decir, tres veces el área del \(n\)-gono generador. ■
Ahora nos ocupamos de la longitud de la cicloide poligonal.
Teorema 4.12.
Cuando un polígono regular rueda a lo largo de una recta, la longitud de la cicloide poligonal generada por uno de sus vértices es cuatro veces la suma de los radios de la circunferencia circunscrita al polígono.
Demostración.
(Mallinson, 1998b). Tratamos de forma separada los casos \(n\) par y \(n\) impar. Para ambos, dibujamos rombos cuyos lados miden lo mismo que los lados del \(n\)-gono, y cuyas diagonales son lados de la cicloide poligonal. Es posible colocar estos rombos dentro del \(n\)-gono de forma que se ve que la suma de las longitudes de los lados de la cicloide poligonal es cuatro veces la suma de los radios inscrito y circunscrito del \(n\)-gono generador. En la Figura 4.22 ilustramos el caso \(n = 10\); y en la Figura 4.23, el caso \(n = 9\). ■
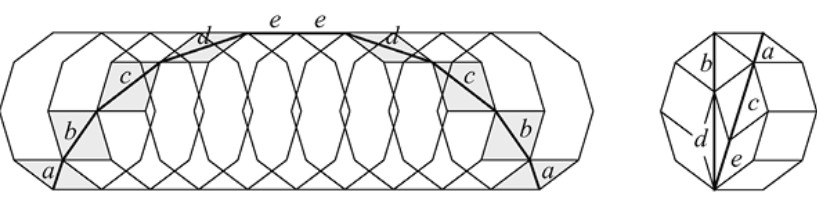
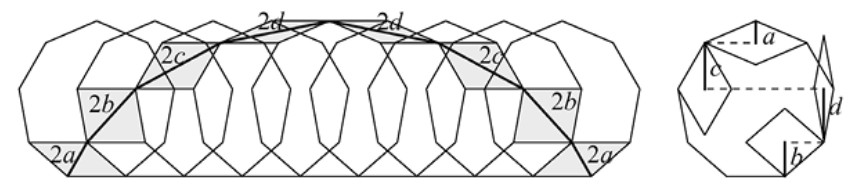
Se puede calcular fácilmente el área limitada por un ciclogono y la recta sobre la que se hace rodar el polígono que lo genera usando métodos similares a los utilizados en la demostración del Teorema 4.11. Véase, por ejemplo (Apostol y Mnatsakanian, 1999).
Teorema 4.13.
Cuando un polígono regular rueda a lo largo de una recta, el área del ciclogono generado por un vértice del polígono es igual al área del polígono más dos veces el área de su círculo circunscrito.
4.9. Desafíos
4.1. Sea \(n \ge 3\), si \(p_n\) y \(P_n\) (\(a_n\) y \(A_n\)) son, respectivamente, los perímetros (áreas) de los \(n\)-gonos regulares inscrito y circunscrito a una misma circunferencia, probar que
4.2. Probar que el área \(a_{2n}\) del \(2n\)-gono regular inscrito en la circunferencia unidad es numéricamente la mitad del perímetro \(p_n\) del \(n\)-gono regular inscrito.
4.3. Si \(p_k\) y \(P_k\) son, respectivamente, los perímetros de los \(k\)-gonos inscrito y circunscrito a una misma circunferencia, probar que
4.4. En los teoremas de Maekawa y Kawasaki sobre origami plano no se dice que el número de pliegues-valle y pliegues-montaña y los ángulos entre ellos son cruciales, pero también lo es el orden en que los dobleces aparecen alrededor del vértice. El patrón que se ve plegado en la Figura 4.24a puede ser desplegado, como se ve en la Figura 4.24b, pero el patrón de la Figura 4.24c, no. ¿Por qué no?
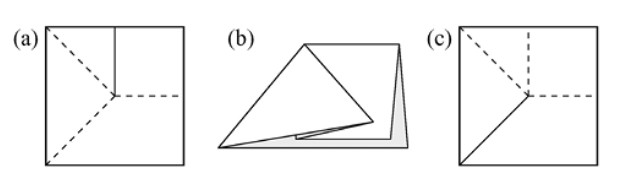
4.5. Sea \(P_n\) el perímetro de un \(n\)-gono regular inscrito en una circunferencia de radio \(r\). Usar que \(\displaystyle \lim_{n\to\infty} P_n = 2\pi r\) para demostrar que \(\displaystyle \lim_{\theta\to 0} \frac{\sin \theta}{\theta} = 1\).
4.6. Probar que la suma de los ángulos de los vértices situados en las puntas del polígono regular estrellado \(\{p/q\}\) es \((p - 2q)\cdot 180^\circ\).
4.7. Sea \(P\) un \(n\)-gono regular con radio circunscrito \(R\). Probar que la suma de los cuadrados de las longitudes de todos sus lados y de todas sus diagonales es \(nR^2\).
4.8. En un \(n\)-gono convexo dado, sea \(T_n\) el número de triangulaciones del polígono. Probar que \(T_n \ge 2 T_{n-1}\) y \(T_n \ge 2^{\,n-3}\).
4.9. ¿Cuánto miden los ángulos de la cicloide poligonal generada por un \(n\)-gono al rodar sobre una recta?
4.10. Sea \(Q\) un punto situado en el interior o en el perímetro de un \(n\)-gono regular. Probar que la suma de todas las distancias de \(Q\) a los lados del polígono es constante. (Indicación: la constante es veces el radio de la circunferencia inscrita en el \(n\)-gono.)
4.11. (a) Probar que un hexágono regular, seis cuadrados y seis triángulos formulauiláteros pueden ensamblarse sin superposición para formar un dodecágono regular. (b) Sean \(V_1, V_2, \dots, V_{12}\) los vértices sucesivos de un dodecágono regular. Estudiar la intersección de las mediatrices de las líneas de las tres diagonales \(V_1V_9\), \(V_2V_{11}\) y \(V_4V_{12}\). (problema 1-I de la 24th Annual William Lowell Putnam Mathematical Competition, 1963).
Capítulo 5 — Un tesoro de teoremas sobre triángulos
El único camino de reyes hacia la Geometría Elemental es el ingenio.
Eric Temple Bell
Este autor confiesa humildemente que para él la Geometría es,
verdaderamente, una rama del Arte.
Julian L. Coolidge
El libro I de los Elementos de Euclides está dedicado a los teoremas sobre rectas paralelas, áreas y triángulos. De las cuarenta y ocho proposiciones de este libro, veintitrés tratan sobre triángulos. La proposición 47 es el teorema más conocido de las matemáticas, el teorema de Pitágoras. En consecuencia, uno podría afirmar justificadamente que los triángulos se hallan en el corazón de la Geometría.
Comenzamos este capítulo con varias demostraciones del teorema de Pitágoras seguidas por algunos resultados emparentados, entre ellos la generalización de Pappus del teorema pitagórico. Apoyándonos en la circunferencia inscrita y la circunferencia circunscrita en un triángulo, llegaremos a la fórmula de Herón y a la desigualdad de Euler. Concluiremos el capítulo con la desigualdad de Erdős–Mordell, el teorema de Steiner–Lehmus, algunos resultados sobre las medianas de un triángulo y un problema de Lewis Carroll.
5.1. El teorema de Pitágoras
Como se mencionó en la introducción, seguramente hay más demostraciones del teorema de Pitágoras que de cualquier otro teorema matemático. El clásico libro The Pythagorean Proposition de Elisha Scott Loomis (Loomis, 1968) presenta literalmente cientos de demostraciones. La página web del académico Alexander Bogomolny, Interactive Mathematics Miscellany and Puzzles contiene ciento veintidós demostraciones (a fecha de diciembre de 2019), muchas de ellas interactivas. Se puede argumentar que la mejor demostración es la de Euclides. El teorema aparece en la proposición 47 del libro I de los Elementos (Joyce, 1996):
En un triángulo rectángulo, el cuadrado construido sobre el lado opuesto al ángulo recto es igual a la suma de los cuadrados construidos sobre los lados que forman el ángulo recto.
La técnica de demostración combinatoria de doble recuento se puede extender para áreas: calcular el área de una región de dos maneras diferentes nos debe llevar al mismo resultado. Esta extensión del principio de Fubini se usa en otra clásica demostración del teorema de Pitágoras basada en una que aparece en el Zhou bi suan jing, un manuscrito chino fechado unos 200 años a. C. (Véase la Figura 5.1).
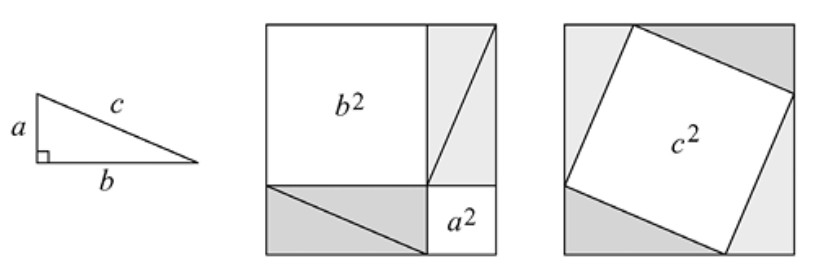
Para un triángulo rectángulo de catetos a y b e hipotenusa c, expresamos el área del cuadrado de lado a + b de dos formas diferentes para llegar a a² + b² = c².
Otra forma de usar la extensión del principio de Fubini para probar el teorema de Pitágoras es por disección: cortar los cuadrados de áreas a² y b² en varias piezas, y reagruparlas formando con ellas un cuadrado de área c². Se suele atribuir la demostración por disección de la Figura 5.2a a Anarizdi de Arabia (ca. 900 d. C.), mientras que la de la Figura 5.2b se atribuye a Henry Perigal (1801–1899).
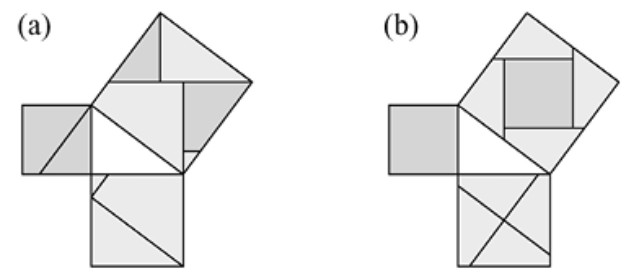
5.2. Parentescos pitagóricos
En este apartado presentamos algunos resultados emparentados con el teorema de Pitágoras.
Teorema 5.1 — El teorema de Pitágoras de los inversos.
Si \(a\) y \(b\) son los catetos y \(h\) la altura levantada sobre la hipotenusa de un triángulo rectángulo, entonces
Demostración.
Sea \(c\) la hipotenusa. Calculando el área del triángulo original de dos formas diferentes, se obtiene \(ab/2 = ch/2\), de donde \(c/(ab) = 1/h\). Y como
Observación. Los triángulos rectángulos de catetos \(a, b\) y de catetos \(1/a, 1/b\) son semejantes, y la hipotenusa del segundo es el inverso de la altura del primero desde su hipotenusa \(c\).
Generalización (añadida, no viene en el libro).
Si \(a\), \(b\) y \(c\) son los catetos de un tetraedro rectángulo y \(h\) la altura levantada sobre la cara formada por los tres catetos, entonces
Demostración.
Una generalización del teorema de Pitágoras nos dice que la suma de los cuadrados de las caras catetos de un tetraedro rectángulo es igual al cuadrado del área de la otra cara (cara hipotenusa)
Calculando el volumen del tetraedro de dos formas diferentes, se obtiene \(abc = Ah\), de donde \(A/(abc) = 1/h\). Y al dividir ambos miembros de (1) por \((abc)^2\) concluimos.
Identidades geométricas para una base ortogonal \(u_1,\dots,u_n\)
Sea \(\{u_1,\dots,u_n\}\) una base ortogonal de \(\mathbb{R}^n\). Denotamos por \(\|u_i\|\) el módulo (norma euclidiana) de \(u_i\). A continuación aparecen tres afirmaciones con sus fórmulas y una demostración breve en el caso ortogonal.
Notación
- \(\|u_i\|\) es la norma de \(u_i\). - \(d\) será la longitud de la diagonal del ortoedro cuyos aristas son los vectores \(u_1,\dots,u_n\). - Sea \(\Delta\) el \((n-1)\)-simplex (o, dicho de otra forma, el polígono convexo de dimensión \(n-1\)) determinado por los puntos extremos \(u_1,\dots,u_n\). Denotamos por \(\mathrm{Vol}_{n-1}(\Delta)\) su \((n-1)\)-volumen (área si \(n=3\), longitud si \(n=2\), etc.). - \(h\) será la altura (distancia euclidiana) desde el origen \(O\) al hiperplano afín que contiene los puntos \(u_1,\dots,u_n\).
1) Diagonal del n-ortoedro
La diagonal \(d\) del ortoedro definido por las aristas ortogonales \(u_1,\dots,u_n\) satisface
2) Relación con el \((n-1)\)-volumen del hiperplano de los extremos
Para cada \(i\) definimos el área (o \((n-1)\)-volumen) del paralelogramo que resulta al omitir \(u_i\) Entonces se cumple la identidad
Obs.: la igualdad final expresa la relación entre la suma de los cuadrados de las áreas de las \((n-1)\)-caras coordenadas y el cuadrado del \((n-1)\)-volumen del simplex \(\Delta\) cuyos vértices son \(u_1,\dots,u_n\). Para comprobar la consistencia en dimensiones bajas:
- \(n=2\): la suma es \(\|u_2\|^2+\|u_1\|^2\), que coincide con la longitud al cuadrado del segmento entre \(u_1\) y \(u_2\).
- \(n=3\): la suma \(\|u_2\|^2\|u_3\|^2+\|u_1\|^2\|u_3\|^2+\|u_1\|^2\|u_2\|^2\) es \(4\) veces el cuadrado del área del triángulo con vértices \(u_1,u_2,u_3\) (ya que \((n-1)! = 2\) cuando \(n=3\)).
3) Relación entre las normas inversas y la altura \(h\)
Sea \(h\) la distancia desde el origen al hiperplano afín que contiene los puntos \(u_1,\dots,u_n\). Entonces se cumple
Teorema 5.2 — Teorema de tipo Pitágoras (Hoehn, 2000).
En un triángulo isósceles, sea \(c\) la longitud de los lados iguales. Dibujemos un segmento de longitud \(a\) desde el ápice hasta la base, dividiéndola en dos segmentos de longitudes \(b\) y \(d\), como se muestra en la Figura 5.3a. Entonces, \(c^2 = a^2 + bd\).
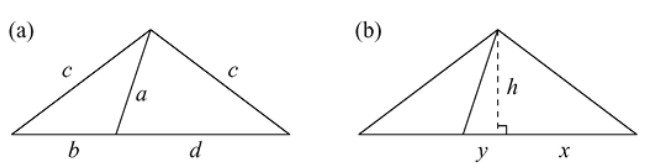
Demostración.
Sea \(h\) la altura del triángulo, y sean \(d = x + y\) y \(b = x - y\), como se ve en la Figura 5.3b. Aplicando dos veces el teorema de Pitágoras, \(c^2 = h^2 + x^2\) y \(a^2 = h^2 + y^2\), luego \(c^2 = a^2 + x^2 - y^2\). Como \(x^2 - y^2 = (x + y)(x - y) = bd\), obtenemos el resultado.
Teorema 5.3 — Teorema de la bisectriz del ángulo recto (Eddy, 1991).
La bisectriz interior del ángulo recto de un triángulo rectángulo divide por la mitad el cuadrado construido sobre la hipotenusa (véase la Figura 5.4).
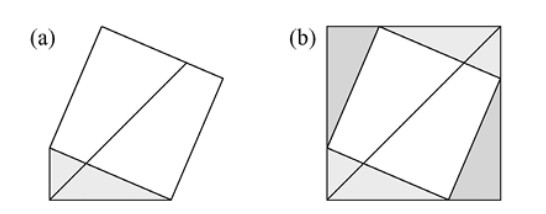
Demostración.
Véase la Figura 5.4b, que forma parte de la demostración del teorema de Pitágoras del Zhou bi suan jing (Figura 5.1). El dibujo muestra que la bisectriz del ángulo recto pasa por el centro del cuadrado construido sobre la hipotenusa.
Es fácil probar que los únicos triángulos rectángulos cuyos lados están en progresión aritmética son los semejantes al triángulo rectángulo 3,4,5. ¿Qué podemos decir si pedimos que los lados estén en progresión geométrica? El siguiente teorema nos da la (algo) sorprendente respuesta (Herz–Fischler, 1993). La demostración se obtiene directamente del teorema de Pitágoras.
Teorema 5.4.
Los lados de un triángulo rectángulo están en progresión geométrica si y sólo si el triángulo es semejante al que tiene lados \(1\), \(\sqrt{\varphi}\) y \(\varphi\), siendo \(\varphi\) la proporción áurea.
Johannes Kepler (1571–1630) escribió los siguiente: “Hay dos grandes tesoros en la Geometría: uno es el teorema de Pitágoras; el otro la división de un segmento en media y extrema razón (es decir, en proporción áurea). Podemos comparar el primero con un pedazo de oro, el segundo es una preciosa joya”. Los triángulos del Teorema 5.4 son a menudo llamados triángulos de Kepler, ya que en ellos aparecen los dos tesoros citados por el matemático alemán.
Los triángulos de Kepler y la Gran Pirámide
La Gran Pirámide de Keops en Giza (Egipto) ha sido fuente de muchas especulaciones y en ella podemos encontrar sorprendentes coincidencias. Algunos entusiastas de las pirámides sostienen que la Gran Pirámide fue construida de forma que el área de cada una de las caras triangulares fuera igual al cuadrado de su altura (véase la Figura 5.5). Si esto fuera verdad, entonces llamando a la mitad del lado de la base cuadrada, h la altura y s la altura de una cara triangular, se tendría que
\[ \frac{bs}{2} = h^{2} \qquad \text{y} \qquad s^{2} = h^{2} + \left(\frac{b}{2}\right)^{2}. \]
Tomemos por conveniencia \(b = 2\), de forma que \(s = h^2\), \(s^2 = h^2 + 1\), y entonces \(s^2 = s + 1\). Por tanto, s será el número de oro y el triángulo rectángulo sombreado en la Figura 5.5, de lados s, \(b/2\) y h, un triángulo de Kepler.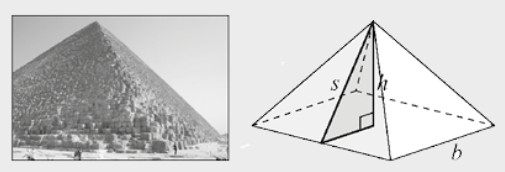
Otros místicos de las pirámides proclaman que la Gran Pirámide fue construida de forma que el perímetro de la base fuera igual al de la circunferencia de radio igual a la altura, es decir, \(b = 4h\). En ambas aseveraciones fleuran ciertas (el 1% y 0.1%, respectivamente):
con \(b = 2\) y \(h = \sqrt{\varphi}\) tendríamos
\(\pi = 4\sqrt{\varphi} \approx 3.1446\), lo que es una aproximación de π con un error menor del 0.1%, uno de los errores más pformulaueños conocidos (Peters, 1978). Para otras relaciones entre π y φ, véase el Apartado 12.3.